Course Description
We will study a number of computational tools and techniques to model and visualize scientific processes. Each sessions we will carry out a series of computational exercises using Mathematica, matlab, Python, C, Fortran, and/or a computer language of the student’s choice (no previous programming experience is required). These exercises will be drawn from mathematics, chemistry, biology, and physics. In addition, we will have a quick introduction to the typesetting program LaTeX, allowing for the preparation of professional scientific documents incorporating high-quality images. An effort will be made to allow each student to work on problems appropriate to his or her interests.
Course Documents
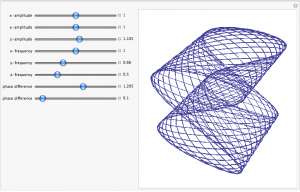 Qiao Zhang, Art Machine
Qiao Zhang, Art Machine
This visualization project is inspired by the Double Pendulum device constructed by Professor R. H. Romer from Amherst College. The Double Pendulum, dubbed “the Art Machine”, produces intriguing Lissajous ï¬gures on paper. We will ï¬rst replicate the curious patterns produced by Prof. Romer’s “the Art Machine”, and then extend to cases that are constrained by limitations of the experimental apparatus.
Useful Links for Python
- Python Definitive Website and Documentation
- A Byte of Python A very nice intro to Python
- Quick Python Tutorials Another nice intro to Python
- Minimal Python for Scientific Computing A nice short intro
- Python Programming More detailed documentation
- How to Think Like a Computer Scientist A full book, using Python
- SciPy Scientific Computing Tools for Python
- Matplotlib Nice Plotting Tools for Python
- Enthought A nice comprehensive distribution of Python, SciPy, Matplotlib, and more
- SciPy Course Outline An online course for SciPy and Matplotlib
- Scientific Computing with Python Online presentations
Other Useful Links
- Fortran Tutorial
- Fortran Programming Tutorial
- GNU Fortran A free Fortran compiler
- C Programming
- Mathematica Tutorials
- Hands-on Start to Mathematica Video
- Hands-on Start Part 2
- Mathematica Video Collection
- Wolfram Demonstrations Project
- Basic MATLAB Tutorial
- More MATLAB Tutorials
- MATLAB Demos
- LaTeX Tutorial
- TeXShop Installation (for Mac)
- TeX Installation (for PC)
- Visualization Toolkit
- MayaVI