Sectors with Density in Granada
My undergraduate research Geometry Group and I have been having a great summer here in Granada Spain. We’ve been considering planar sectors of angle with density
and the isoperimetric problem: to enclose given weighted area with least weighted perimeter. We’ve proved that there are angles
such that the minimizer is:
1. for , a circular arc about the origin;
2. for , an unduloid (half-period of a periodic curve normal to both edges of the sector);
3. for , a semicircle through the origin.
We have lots of evidence that and
, but we have not been able to prove it. Can you help us? Check out our arXiv post.
 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the
Sean Howe:
Right now we know that for density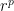 the circular arc minimizes up until the π/(p+1) sector. We could improve that to the π/(p/2+1) sector if we could show that in the plane with regular area and perimeter density
the circular arc minimizes up until the π/(p+1) sector. We could improve that to the π/(p/2+1) sector if we could show that in the plane with regular area and perimeter density  for
for  circles about the origin were minimizers. Indeed, the entire conjecture has an equivalent statement in terms of the plane with different area and perimeter densities, but this is a particularly nice case. Furthermore the line p/2+1 is the tangent line at p=0 to √(p+1) so this is the best possible linear (in the denominator) estimate we could get.
circles about the origin were minimizers. Indeed, the entire conjecture has an equivalent statement in terms of the plane with different area and perimeter densities, but this is a particularly nice case. Furthermore the line p/2+1 is the tangent line at p=0 to √(p+1) so this is the best possible linear (in the denominator) estimate we could get.
19 July 2009, 11:15 amFrank Morgan » Blog Archive » Manifolds with Density: Fuller References:
[…] [2012] Alexander Díaz, Nate Harman, Sean Howe, David Thompson, Isoperimetric problems in sectors with density, Adv. Geom. 12 (2012), 589–619; arXiv.org (2010); see blog posts 1 and 2. […]
21 October 2014, 4:46 am