29th October 2009, 05:46 am
Note added 13 June 2017: see a video featuring Prof. Johnson at the NESN Clubhouse.
In his senior colloquium last fall advised by Frank Morgan, Davide Carozza ’09 investigated the fastest path around the bases in baseball, assuming a bound of say 10 ft/sec2 on acceleration/deceleration. Following the baseline, stopping at each base, takes about 22.2 seconds. The standard recommended “banana” path follows the baseline maybe halfway to first base and then veers a bit to the right to come at first base from a better angle to continue towards second. That cannot be ideal. It would have been better to start at an angle to the right to head directly to an outer point on the banana path. Davide found that a circular path at 17.8 seconds is roughly 20% faster than following the baseline at 22.2 seconds. Stewart Johnson then computed the following optimal path at 16.7 seconds. The record time according to Guiness is 13.3 seconds, set by Evar Swanson in 1932 (with larger acceleration than our assumed 10 ft/sec2).
17th October 2009, 08:43 am
The celebrated Gauss-Bonnet formula has a nice generalization to surfaces with densities discovered by my 2004 undergraduate research Geometry Group. The classical Gauss-Bonnet formula relates the integral of the Gauss curvature G over a disc D to the integral over its boundary of the geodesic curvature  :
:
 .
.
One can weight arclength and area by densities:
 .
.
Surfaces with density appear throughout mathematics, including probability theory and Perelman’s recent proof of the Poincaré Conjecture (see Chapter 18 of the 2009 edition of my Geometric Measure Theory book). Important examples include quotients of Riemannian manifolds by symmetries and Gauss space, defined as Rn with Gaussian density c exp(-r2).
The generalized Gauss curvature is given by
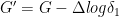 .
.
Ivan Corwin and I have just written an article about this. The formula for how Gauss curvature changes under a conformal change of metric is a simple special case.
15th October 2009, 09:25 am
Write-up of a departmental faculty seminar, October 2, 2009.
Solutions to problems in geometry and physics and even in the social sciences tend to be symmetric. As prime example, the solution to the isoperimetric problem, which seeks the least-perimeter way to enclose given volume in R3, is a sphere, the most symmetric of all shapes. One way to prove this is to show that anything else improves as you make it more symmetric. For thousands of years, mathematicians have been looking for good ways to make shapes more symmetric and to prove that as they get more symmetric they “get better,” for example, enclose the same volume with less perimeter.
My favorite references are Burago and Zalgaller [BZ, §9.2] and Ros [R1, §3.2]. This talk is based on [MHH]. Gromov [G, §9.4] provides some sweeping remarks and generalizations, including most of our results.
1. Steiner symmetrization [St, 1838] replaces every vertical slice of a region in R3 with a centered interval of the same length, as in Figure 1. By calculus, the volume does not change, but one can show that the perimeter decreases (or remains the same).
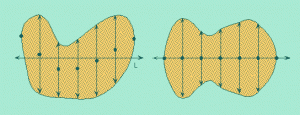
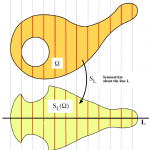
Figure 1. Steiner symmetrization replaces every vertical slice with a centered interval of the same length. www.math.utah.edu/~treiberg/Lect.html
Continue reading ‘Symmetrization’ »



 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the