Frank Morgan

Write-up of a departmental faculty seminar, October 2, 2009.

Solutions to problems in geometry and physics and even in the social sciences tend to be symmetric. As prime example, the solution to the isoperimetric problem, which seeks the least-perimeter way to enclose given volume in R³, is a sphere, the most symmetric of all shapes. One way to prove this is to show that anything else improves as you make it more symmetric. For thousands of years, mathematicians have been looking for good ways to make shapes more symmetric and to prove that as they get more symmetric they “get better,” for example, enclose the same volume with less perimeter.

My favorite references are Burago and Zalgaller [BZ, §9.2] and Ros [R1, §3.2]. This talk is based on [MHH]. Gromov [G, §9.4] provides some sweeping remarks and generalizations, including most of our results.

1. Steiner symmetrization [St, 1838] replaces every vertical slice of a region in R³ with a centered interval of the same length, as in Figure 1. By calculus, the volume does not change, but one can show that the perimeter decreases (or remains the same).

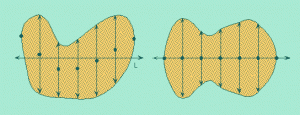
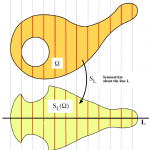
Figure 1. Steiner symmetrization replaces every vertical slice with a centered interval of the same length. www.math.utah.edu/~treiberg/Lect.html

2. Schwarz Symmetrization [Sc, 1884] replaces every horizontal slice of a region in R³ with a centered round disc of the same area. Again, volume does not change, but the perimeter decreases or remains the same.

Figure 2. Schwarz symmetrization replaces horizontal slices with centered round discs. www.toy-library.com.au/quoits.gif, danbrunskill.blogspot.com/2009/03/imhotep.html, Gatlinburg Trail April 2017

3. Generalized Schwarz Symmetrization.  Steiner and Schwarz symmetrization can be generalized to any product BxRⁿ of a Riemannian manifold B with Rⁿ, replacing every vertical slice in Rⁿ of a region with a centered round ball of the same volume. Our two original examples wereR²xR¹ (Steiner symmetrization) and R¹xR² (Schwarz symmetrization). More generally, one can replace BxRⁿ with BxSⁿ or BxF for any Riemannian manifold F in which balls about some fixed point are perimeter minimizing.

4. Warped Products. More generally, symmetrization generalizes to a warped product Bx_gF, in which each fiber {b}xF is scaled by a factor g(b), so that the metric takes the form

ds² = db² + g(b)²dt².

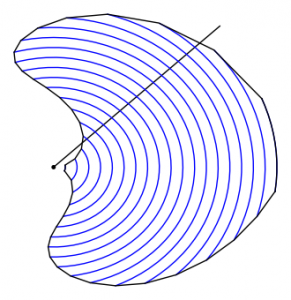
A prime example is roughly to view R³ as a warped product R⁺x_bS², in which the fibers are concentric spheres about the origin parameterized by their intersection with the positive x-axis. Each such spherical fiber is scaled up by its distance b from the origin. Symmetrization replaces the intersection with each such spherical fiber by a spherical cap of the same area centered on the x-axis. This particular symmetrization is called spherical symmetrization. Spherical symmetrization is traditionally viewed as distinct from Schwarz symmetrization, but now we see that it is just generalized Schwarz symmetrization on a particular warped product.

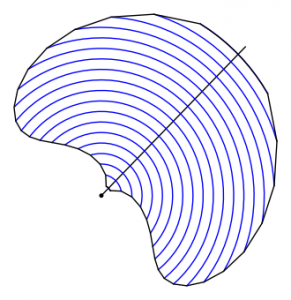
Figure 3. Spherical symmetrization replaces the intersection with a sphere with a spherical cap. Image by Sean Howe.

5. Fiber Bundles. More generally, symmetrization generalizes to fiber bundles.  By definition, a Riemannian fiber bundle M with base B is a Riemannian manifold together with a “projection” map P onto another Riemannian manifold B. Each inverse image P^–1(p) is called a fiber. We will be interested in the case when the projection is a Riemannian submersion, which means that infinitesimally the restriction of P to the orthogonal complement of a fiber is an isometry, and when each fiber is a scaling of a fixed Riemannian manifold F. The simplest and most famous example is the Hopf fibration P:S³->S² with unit circle fibers. Think of S³ in R⁴ = C², which has isometries of the form

(z₁, z₂) -> (e^itz₁, e^itz₂) ,

simultaneous identical rotation in each complex line. The fibers of S³ are the orbits of these isometries. Even locally S³ is not a Riemannian product B²xS¹; instead, nearby fibers spiral around a given fiber. And globally S³ is not even topologically the same as S²xS¹.

Unfortunately there’s no way in general to define symmetrization in the fiber bundle, because there’s no B inside the fiber bundle for centering the symmetrization.* Instead, the symmetrization is defined in the associated warped product Bx_gF. It works under the additional hypothesis that infinitesimally horizontal translation scales volume.

Ros [R2] used fiber bundle symmetrization for Hopf fibrations to solve the isoperimetric problem in certain lens spaces.

6. Densities. More generally, symmetrization generalizes to densities [M, Chap. 18].

7. Open Question. Unfortunately, symmetrization does not seem to work for example in R² with density exp(r⁴) = exp((x²+y²)²), because the horizontal translation does not preserve or scale volume. It remains an open conjecture that balls about the origin are isoperimetric. The conjecture applies to any log convex radial density on R^N. See [RCBM, Conj. 3.12].

Acknowledgements. This write-up of a departmental faculty seminar is based on joint work with Sean Howe and Nate Harman [MHH], which began with the Williams College, National Science Foundation SMALL undergraduate research Geometry Group at the University of Granada, Spain, summer 2009. We would like to thank Vincent Bayle, Antonio Cañete, Alexander Díaz, Rafael López, Manuel Ritoré, Antonio Ros, César Rosales, and David Thompson for help and inspiration. We acknowledge partial support by the National Science Foundation (grants to Morgan and to the SMALL REU), the Spanish Ministerio de Educación y Ciencia (grant to Ritoré, Rosales, et al.), the University of Granada, and Williams College. We would be grateful for comments on our preprint [MHH].

References

[BZ]          Yu. D. Burago and V. A.  Zalgaller, Geometric Inequalities, Springer-Verlag, 1980.

[G]            M. Gromov, Isoperimetry of waists and concentration of maps, Geom. Funct. Anal. 13 (2003), 178–215.

[MHH]      Frank Morgan, Sean Howe, and Nate Harman, Steiner and Schwarz symmetrization in warped products and fiber bundles with density, arXiv.org (2009).

[R1]           Antonio Ros, The isoperimetric problem, Global Theory of Minimal Surfaces (Proc. Clay Math. Inst. Summer School, 2001), Amer. Math. Soc., Providence, RI (2005), 175-207.

[R2]           Antonio Ros, The isoperimetric problem for lens spaces, in preparation.

[RCBM]           César Rosales, Antonio Cañete, Vincent Bayle, and Frank Morgan, On the isoperimetric problem in Euclidean space with density, Calc. Var. PDE 31 (2008), 27-46.

[Sc]           H. A. Schwarz, Beweis des Satzes, dass die Kugel kleinere Oberfläche besitzt, als jeder andere Körper gleichen Volumens, Nachrichten Königlichen Gesellschaft Wissenschaften Göttingen (1884), 1–13.

[St]            J. Steiner, Einfache Beweise der isoperimetrischen Hauptsatze, Crelle’s J. 18 (1838), 286-287.

*Note on Section 5 added March, 2011. Daniel John did the best you can to define symmetrization inside symmetric spaces of noncompact type.

Note: Steiner and Schwarz symmetrization fail for non-product densities f on Rⁿ.

Note: For the ultimate analysis of equality, see Cagnetti et al., 2013. Earlier results on spherical symmetrization appear in Morgan-Pratelli [MP, 6.2, 6.4] and Chung et al. [C, 3.8, 3.9].

[C] Ping Ngai Chung, Miguel A. Fernandez, Niralee Shah, Luis Sordo Vieira, Elena Wikner, Are circles isoperimetric in the plane with density e^r? preprint (2011).

[MP] Aldo Pratelli, Existence of isoperimetric regions in Rⁿ with density, Ann. Global Anal. Geom.  43 (2013), 331–365; arXiv.org (2011).