Log-Sobolev Inequality
My 2009 Williams College NSF “SMALL” undergraduate research Geometry Group has the following inequality for any function on the unit interval and for any p ≥ 1:
with equality for constant functions and if p>1 only for constant functions. They conjecture that these results still hold if on the right-hand side is replaced by
(sharp).
The case p=1 is standard and follows from Wirtinger’s Inequality.
Are any inequalities like this known?
 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the
LJS:
Isn’t the LHS decreasing in p, so p=1 is worst case?
This does not of course help with the conjecture.
Right you are, thanks very much. The undergraduates came upon it in a completely different way, as a generalization of the isoperimetric inequality (p=1) to sectors of planes with density , using the four vertex theorem. Your comment inspired a simpler geometric comparison argument. Do you believe the conjecture?—FM
, using the four vertex theorem. Your comment inspired a simpler geometric comparison argument. Do you believe the conjecture?—FM
11 June 2009, 2:36 pmFrank Morgan:
Comment from David Thompson, SMALL undergraduate research Geometry Group ’09
The conjectured inequality says that for all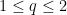 ,
,
The case holds trivially;
case holds trivially; 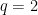 is the standard isoperimetric inequality. Both sides are concave as functions of
is the standard isoperimetric inequality. Both sides are concave as functions of 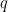 . Would some kind of interpolation argument prove the result for all
. Would some kind of interpolation argument prove the result for all 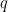 ?
?
14 June 2009, 10:04 amFrank Morgan:
Francesco Maggi at Firenze notes that differentiating with respect to q at q=1 implies the following log-Sobolev inequality for uniform measure on the interval for a nonnegative function f of mean 1:
Corollary of Conjecture: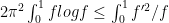 .
.
Similarly the corollary, on small perturbations of f = 1, implies the sharp, known Wirtinger inequality:
![[\int_0^1 u^2\le(1/\pi^2)\int_0^1 (u')^2] [\int_0^1 u^2\le(1/\pi^2)\int_0^1 (u')^2]](https://s0.wp.com/latex.php?latex=%5B%5Cint_0%5E1+u%5E2%5Cle%281%2F%5Cpi%5E2%29%5Cint_0%5E1+%28u%27%29%5E2%5D&bg=ffffff&fg=000000&s=0)
 .)
.)
9 June 2010, 3:29 amfor (nonperiodic) u of mean 0. (For u periodic the sharp constant is
Frank Morgan:
My 2012 undergraduate research Geometry Group has observed that the sharp log-Sobolev inequality on the interval follows immediately from a similar inequality on the circle.
30 August 2012, 5:17 amFrank Morgan » Blog Archive » Manifolds with Density: Fuller References:
[…] [2012] Alexander Díaz, Nate Harman, Sean Howe, David Thompson, Isoperimetric problems in sectors with density, Adv. Geom. 12 (2012), 589–619; arXiv.org (2010); see blog posts 1 and 2. […]
17 October 2014, 9:16 am