Math, Teaching, and Other Items of Interest
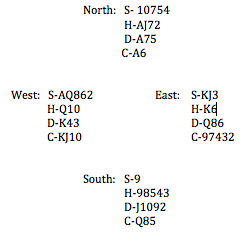
My mom and I just had a great time on the first ACBL Regional at Sea, an Alaskan cruise with the inimical Billy Miller. My mom won enough gold points to become a Life Master. In that fateful session Thursday afternoon, July 18, 2013, as West she played one hand at 3N which should only make 2N and she somehow made 5N:
Continue reading ‘Alaskan Bridge Cruise with Billy Miller’ »
Jian Ge’s recent ArXiv post on “Comparison theorems for manifolds with mean convex boundary,” Theorem 0.1, has a generalization to manifolds with density, here within a factor of 2 of sharp for constant density: Continue reading ‘Distance to Boundary of Manifold with Density’ »
In Rn or in a Riemannian manifold, one may consider regions R with density given by an integrable nonnegative function g, with volume ∫R g. If everything is smooth, the perimeter is given by ∫∂R g, or more generally by Stokes’ Theorem. For finite perimeter, these are the so-called normal currents of geometric measure theory. All of this can be done in a manifold with density f (unrelated to g).
In Rn, if you allow regions with density, there is no isoperimetric optimum for given volume, because large balls with low (constant) densities approach perimeter 0; similarly in any space for which P/V has no minimum. In a space of finite volume, such as Gauss space Gn (Rn with Gaussian density) there is an optimum: the whole space with appropriate constant density has perimeter 0. At the other extreme, in R with density exp(x3), a left halfline with high density approaches perimeter 0.
Note that if a region with density is isoperimetric, it remains so for all multiples of that density.
In principle one may allow regions with variable density f, the variability contributing to the boundary, but since any such region is an integral of regions Rd = {f ≥ d} with constant density d, one need consider only regions with constant density.
For a manifold with density with isoperimetric profile P = I(V), the least-perimeter region with density with unit volume just minimizes cI(1/c); in a space of infinite volume its perimeter to volume ratio is the Cheeger constant inf P/V.
In R2 with density exp(r2), where classical isoperimetric regions are balls about the origin, among regions with density the isoperimetric optimum for every area is the same disc of radius r ~ 1.1 (solution to exp(r2) = 2r2 + 1) with appropriate constant density.
Proposition. In Rn with smooth, uniformly log-convex radial density f(r), an isoperimetric region with density exists.
Guest post by Neeko Gardner, Caroline Atwood, Paul Friedrich, Llewellyn Smith
On Saturday, February 16th, the recently formed Williams College bridge team participated in the collegiate qualifying bridge tournament online on bridgebase. Having just come off an intensive month-long winter study class on bridge, we decided to test our newfound skills against other collegiate teams. We were up against Stanford, UPenn, CalTech, Hamilton, UChicago, Cornell, Dartmouth, NYU, and UWashington. Our first round we lost to Dartmouth, then beat NYU, tied against Hamilton, beat Stanford, and lost to UPenn in the final round. With our final loss to Penn who was playing precision and had been partners for over 5 years, we barely lost out qualifying. It was a great showing for Williams, and considering we’d only been playing for a month we did very well. Next year we hope to come back even stronger and qualify. Here’s an interesting hand from our match against Hamilton: Continue reading ‘Williams at Collegiate Bridge Tournament’ »
Participated in the excellent Moravian College Student Mathematics Conference February 16, 2013. Many thanks to my hosts Nate Shank and Kevin Hartshorn, Dean Gordon Weil, student presider Eric Sullivan, and all workers and speakers.
Here in Williamstown we got just about a foot of snow.
Every January Williams students take one special course. Faculty, every other year, teach whatever they like. In 2013 for the second time I taught “Tournament Bridge.” The five first- and second-year students and I studied, practiced, and played in tournaments in Pittsfield, Newton, Rye, and Schenectady.
Paul Freidrich, Neeko Gardner, Ben Hoyle, Professor Frank Morgan, Caroline Atwood, and Llewellyn Smith at the Rye Regional
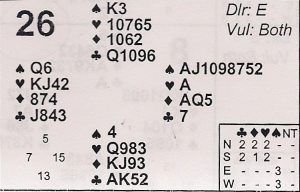When I was at the Field’s Institute in Toronto on sabbatical in the fall of 2010, I played duplicate bridge with 25 different partners. Here’s an interesting hand from Hazel’s Bridge Club on September 6, with Joyce Fraser. I was East at 4S. Do you see how to make it? The key after taking the heart ace is to force an entry to dummy by leading a low spade to the 6. This was good for 10/15 matchpoints.
Actually it can be set by perfect defense. Do you see how? South has to underlead the AK of clubs to North’s Q, so that North can return a diamond to eventually score two diamond tricks.
Here’s an interesting hand from a Royal Caribbean regional bridge tournament cruise (with 6000 passengers and 2000 staff on the Allure of the Seas) with Larry Cohen in December, 2012. After my partner (Lois Hausman) opened 1D, I took her to 6N. After a heart lead, she properly advanced the 9 of spades and West properly covered, leaving East with the J86 after dummy’s A1075. Do you see how to make the hand? Take the club finesse and the AK, play out the red winners, and then put East in with the club 9 to his 10. Now he must lead from his spades. Continue reading ‘Royal Caribbean Bridge with Larry Cohen and Jeff Meckstroth’ »
An ingredient in proving the existence of isoperimetric regions and clusters of prescribed volume(s) is the boundedness of isoperimetric regions of smaller volume(s). One proof of boundedness is by monotonicity. The proof in my Geometric Measure Theory book (Lemma 13.6) uses a non-sharp isoperimetric inequality for small volume and has the advantage of applying to convex integrands more general than area; the requisite isoperimetric inequality follows immediately from the isoperimetric inequality for area. All of this works equally well in the presence of a density. For more delicate results see
Frank Morgan and Aldo Pratelli, Existence of isoperimetric regions in Rn with density, Ann. Global Anal. Geom. (2012); arXiv.org (2011)
and Cinti and Pratelli.
My book comments that existence similarly holds in any smooth Riemannian manifold M with compact quotient M/G by a group of isometries. Monotonicity still yields boundedness; even with density (bounded above and below by compactness) the classical mean curvature is bounded and hence classical monotonicity applies. To use my alternate proof, which applies to more general integrands, one needs the isoperimetric inequality for small volume, which follows immediately from such an isoperimetric inequality for area without density. For the latter in a more general setting, see Theorem 2.1 of Morgan and Ritoré “Isoperimetric regions in cones” after Berard and Meyer. In this simpler setting of M/G compact, you can just cover M with congruent balls with a bounded number of balls meeting each point and apply the relative isoperimetric inequality in each ball. Incidentally the same covering can be used to replace the division into cubes in the existence proof 13.7 in my book.
Welcome to my blog. I also have a blog at the