The Log-Convex Density Conjecture
Announcement: proof posted 19 November 2013 by Gregory R. Chambers, student of Regina Rotman and Alex Nabutovsky at Toronto. By spherical symmetrization the problem reduces to planar curves, which he studies very intelligently in great detail. The main idea is that if the generating curve is not a circle about the origin, then from its maximum (on the axis of symmetry) it spirals inward and it eventually turns through 2π before returning to the axis, contradiction. See his 30-second video. “Proof of the Log-Convex Density Conjecture,” J. Eur. Math. Soc. 21 (2019), 2301–2332.
Update August 2, 2022. arXiv:2208.00195. “Approaching the isoperimetric problem in H^m_ℂ via the hyperbolic log-convex density conjecture” by Lauro Silini. Abstract: We prove that geodesic balls centered at some base point are isoperimetric in the real hyperbolic space H^n_ℝ endowed with a smooth, radial, strictly log-convex density on the volume and perimeter. This is an analogue of the result by G. R. Chambers for log-convex densities on ℝ^n. As an application we prove that in the complex and quaterionic hyperbolic spaces, geodesic balls are isoperimetric in a class of sets enjoying a suitable notion of radial symmetry. The hyperbolic plane case was proved by Igor McGillivray: arXiv:1712.07690, “A weighted isoperimetric inequality on the hyperbolic plane.”
Ken Brakke’s Log-Convex Density Conjecture [Rosales et al. Conj. 3.12] says that in Euclidean space with radial log-convex density f(r), balls about the origin are isoperimetric.
A density is just a positive continuous function used to weight volume and perimeter. Log convexity just means that log f is convex. Balls isoperimetric means that any other region of the same weighted volume has no less weighted perimeter.
Log convexity is necessary because it is equivalent to stability. The question is whether it is sufficient.
After the trivial, borderline case of Euclidean space with unit density, the second example was density f(r) = exp(r2) [Borell; see Rosales et al.], proved by Steiner symmetrization, since exp(r2) is a product as well as rotationally symmetric.
The third example was exp(rp) for p ≥ 2 in R2 [Maurmann-Morgan], by comparison with certain classical surfaces of revolution. The cases 1≤ p < 2 remain conjectural. (Corrected on this blog from p ≥ 1 thanks to Ping Ngai Chung, Miguel Fernandez, Niralee Shah, and Luis Sordo.)
The fourth example was large balls in Rn with uniformly log convex density (Kolesnikov-Zhdanov, generalized by Howe), by the Divergence Theorem.
The fifth example was small balls in Rn with uniformly log-convex density or density C2 close to exp(r2) by asymptotic analysis. A. Figalli and F. Maggi, On the isoperimetric problem for radial log-convex densities, preprint (2012).
In addition there are results for densities xnk exp(r2) in a halfspace and x1k1…xnkn exp(r2) in an orthant by studying constant-generalized-curvature curves in the plane and induction by Engelstein et al. [2009] and by Brock, Chiacchio, and Mercaldo [2011, 2012]. More recently there are more general results in convex cones for densities f homogeneous of degree k with f1/k concave such as x1k1…xnkn or √x + √y but not rp via a comparison mapping of constant weighted divergence by Cabré, Ros-Oton, and Serra (arXiv 2012, see an alternative argument for integer homogeneity by Milman below, arXiv 2013, video) and by stability analysis by Cañete and Rosales (arXiv 2013), who also treat negative k. Third, Milman and Rotem (arXiv 2013) observed that such results follow from the Borell-Brascamp-Lieb generalization of Brunn-Minkowski and from new, similar inequalities. Cabré et al. remark that:
After announcing our result and proof…, we have been told that optimal transportation techniques…could also be used to proof weighted isoperimetric inequalities in certain cones. C. Villani pointed out that this is mentioned in the Bibliographical Notes to Chapter 21 of his book [Optimal Transport, Old And New, Springer, 2009]. A. Figalli showed it to us with a computation when the cone is a halfspace {xn > 0} equipped with the weight xnα.
There are a number of interesting examples where the log-convexity hypothesis fails, balls about the origin are unstable, and other isoperimetric regions are known.
In the famous example of Gauss space, isoperimetric regions are half-spaces (see my Geometric Measure Theory book, Chap. 18).
In the plane or space with density rp, p > 0, isoperimetric regions are balls with the origin on the boundary [Dahlberg et al., Tammen et al.]. On the line with density rp, p > 0, double bubbles are two intervals meeting at the origin [Huang et al.].
In the halfplane {y>0} with density yk (k>0), isoperimetric regions are half-discs about points on the x-axis [Maderna and Salsa, Applicable Anal. 12, 1981].
In Rn with density |xn|kexp(-r2), isoperimetric regions are halfspaces [Brock, Chiacchio, and Mercaldo, J. Math. Anal. Appl. 348, 2008].
When rephrased to state that all balls about the origin are isoperimetric if stable, the conjecture naturally generalizes to perimeter density, volume density, or both (different densities on volume and perimeter). Examples are provided by Betta et al. [B], Díaz et al. [D, Prop. 4.21], Howe [H], Alvino et al. [A1, A2, A3], Di Giosia et al. [DH], and Brock and Chiacchio [BC]. Actually [June 22, 2010], stability of balls about the origin is not quite enough; you need to require smoothness or at least log-convexity of the density at the origin. For example, in the plane with density r-2, isoperimetric regions do not exist, and in the plane with density exp(r2-2r+2), isoperimetric regions for small volume are approximately round balls about the minimum density at r = 1. For perimeter density g(r) on Rn+1, the stability condition for balls about the origin is (n/r)g‘ + g” ≥ 0 for r>0; one should further assume that the inequality holds in some sense at 0. The situation is simpler for area density, where the stability condition (area density nonincreasing) trivially implies that balls about the origin are isoperimetric. (These stability conditions follow from the second variation formulae.)
Regularity (12 January 2020). For regularity of isoperimetric sets, see Pratelli and Saracco [PS] and references therein.
[A1] A. Alvino, F. Brock, F. Chiacchio, A. Mercaldo, M.R. Posteraro, Some isoperimetric inequalities on R^N with respect to weights |x|^\alpha, arXiv.org (2016).
[A2] Angelo Alvino, Friedemann Brock, Francesco Chiacchio, Anna Mercaldo, Maria Rosaria Posteraro, On weighted isoperimetric inequalities with non-radial densities, arXiv.org (2018).
[A3] Angelo Alvino, Friedemann Brock, Francesco Chiacchio, Anna Mercaldo, Maria Rosaria Posteraro, The isoperimetric problem for a class of non-radial weights and applications, arXiv.org (2018).
[B] M. F. Betta, F. Brock, A Mercaldo, and M. R. Posteraro, A weighted isoperimetric inequality and applications to symmetrization, J. Inequal. Applns. 4 (1999), 215–240.
[BC] Friedemann Brock, Francesco Chiacchio, Some weighted isoperimetric problems on R^N+ with stable half balls have no solutions, arXiv.org (2019).
[D] Alexander Díaz, Nate Harman, Sean Howe, David Thompson, Isoperimetric problems in sectors with density, Adv. Geom. 12 (2012), 589–619; arXiv.org (2010).
[DH] Leonardo Di Giosia, Jahangir Habib, Lea Kenigsberg, Dylanger Pittman, Weitao Zhu, Balls Isoperimetric in R^n with Volume and Perimeter Densities r^m and r^k, arXiv.org (2019).
[H] Sean Howe, The Log-Convex Density Conjecture and vertical surface area in warped products, Adv. Geom. 15 (2015), 455–468; arXiv.org (2011).
[PS] Aldo Pratelli and Giorgio Saracco, The ε – ε^β property in the isoperimetric problem with double density, and the regularity of isoperimetric sets, Advanced Nonlinear Studies, February, 2020.
Note added 11 February 2011. Manuel Ritoré suggests such a generalization to any rotationally symmetric manifold with density: if spheres about the origin are stationary and strictly stable, they are the only stable stationary surfaces, and therefore isoperimetric regions, if they exist, are balls or annular regions (of course e.g. for Euclidean space with increasing density they would be balls). [False, see note of 24 September 2016 below.]
Note that for the plane with density 1/r2, circles are strictly stable but minimizers don’t exist (go off to infinity). Morgan, Hutchings, and Howards [MHH, §3.4] give an example of a Riemannian plane of revolution for which annuli occur as isoperimetric regions.
[MHH] Frank Morgan, Michael Hutchings, and Hugh Howards, The isoperimetric problem on surfaces of revolution of decreasing Gauss curvature, Trans. Amer. Math. Soc 352 (2000), 4889-4909.
Note added 18 February 2011, revised 12 June 2011. Li et al. [L, Prop. 9.2 (later renumbered 6.2)] note that a smooth density on Rn is radial if and only if spheres about the origin are stationary for given volume. If one allows the density to be singular at the origin, the same argument shows that the density is a product of a function f(r) of r and a function of Θ (Θ in unit sphere), although the stability condition now becomes more complicated, as Antonio Cañete observed, correcting a mistake I made when I first posted this note.
[L] Yifei Li, Michael Mara, Isamar Rosa Plata, and Elena Wikner, Tiling with penalties and isoperimetry with density, Geometry Group report, Williams College, 2010.
Note added 14 May 2010. Steiner and Schwarz symmetrization fail for non-product densities f on Rn, i.e., for all radial densities except C exp(ar2). For example, the counterexample to horizontal Steiner symmetrization in R2 is a thin isosceles trapezoid with very steep sides. Since the perimeter of the top and bottom remain invariant under symmetrization, it suffices to consider the sides. We will take it to be infinitesimally thin and just compare the infinitesimal contributions to perimeter: at the ends of an interval from (a,y) to (b,y) compared to the symmetrized interval from (-c,y) to (c,y). Each is constrained to have the same rate of change of weighted length as y changes:
If g = log f, these integrals equal the integrals of
,
which can be arranged to be unequal unless
,
which would make f a product density. By sloping the trapezoids one way or the other, we obtain that the tangents satisfy
, i.e.,
,
whereas Steiner symmetrization says that the secants satisfy
, i.e.,
.
Plugging that into the first inequality yields
,
which fails for s large (as you can see by squaring both sides).
Note added 2 June 2010. That symmetrization fails for non-product densities was proved by:
M. Francesca Betta, Friedemann Brock, Anna Mercaldo, and M. Rosaria Posteraro, Weighted isoperimetric inequalities on Rn and applications to rearrangements, Math. Nachr. 281, No. 4, 466–498 (2008), Theorem 3.10.
Date: Fri, 7 Dec 2012
From: Emanuel Milman
…It occurred to me that the Cabre-et-al. result [without uniqueness] actually follows from the original result of Lions-Pacella in the non-weighted case when a (alpha) is an integer…. The reason is that one may consider the following convex cone (by 1-homogeneity and concavity of w1/a) in Rn+a:
Ce := {(x,y) : x is in ∑, y is in Ra, |y| ≤ ew1/a} .
Now equip this convex cone with Lebesgue measure. Note that the projection onto the base cone ∑ pushes forward Lebesgue measure onto the measure ceaw, and the isoperimetric minimizers (as a family) on this space are identical to the ones on the rescaled space with density w, in which we are interested. Also, the projection is a 1-Lipschitz map w.r.t. the Euclidean structures on Rn+a and Rn. Consequently, the isoperimetric behaviour can only be better (further away from zero) on the base space. Now by the Lion-Pacella result, we know that the minimizers on the big cone are Euclidean balls. However, these are not the preimages of any set on the base cone ∑ under the projection, so the argument is still not finished. This is where the parameter e comes in: Taking the limit as e->0, it is easy to verify that the ratio between volumes and also between perimeters of the Euclidean minimizer in the big cone Ce and its approximation by a circumscribing and inscribed lift of a Euclidean ball in ∑, are all (1 + o(e)). (This takes about 4 lines to justify, so I omit it here, but it is clear that it should be the case – the maximal vertical angle of the big cone goes to 0 linearly in e). So although there are various factors like ea present, they all cancel out, and the lower bound on the perimeter that we get by applying Lions-Pacella on Ce and scaling by ea, converges to the asserted lower bound by Cabre-et-al. Basically, the Euclidean minimizer in Ce just degenerates into the asserted Euclidean minimizer in ∑…. Such constructions… are more or less standard in the field of convexity (although it took me a while to incorporate e and make the reduction work), but perhaps this reduction step could also be useful in similar situations (one could try to apply it to the numerous list of results you have in your blog on the log-convexity conjecture).
Remark. If you normalize the big cone in your argument with constant density, then I guess you can use a limit argument instead of your approximation argument.–FM
Note added 24/26 September 2016, Granada. The natural generalization of the Log-convex density conjecture described above in the note of 11 February 2011 is false, as shown by the following counterexample. In the counterexample, even though all circles about the origin are strictly stable, the Gauss curvature at some radius rises above its starting value, so that small circles about the origin cannot be isoperimetric.
We’ll describe a smooth surface of revolution with polar coordinates r, θ and metric
.
Let . Then
and the circle about the origin is stable if and only if
. The Gauss curvature
and
and
(see [EMMP, Sect. 6]).
In particular, H and G increase or decrease together, G more slowly when f is large.
Now from the origin start like a sphere of Gauss curvature .1, initially decreasing a tiny bit so that H is slightly less than 1. When f is about 10 (approximately a hemisphere), let G decrease by a larger but still small amount δ. Since for most of the decrease, H decreases much more than G. Next, when f is about say 1/4 (closer to a whole sphere), increase G to .11. Since
, H increases more slowly than G, so stays below its original value of 1. Finally, to make sure that f does not go to 0, let G and H decrease a lot. So even though H stays less than 1 and all circles about the origin are strictly stable, small circles where the Gauss curvature is .11 have less perimeter than ones about the origin of the same area.
If instead of a plane you want a sphere, just reflect across the minimum of f for a example, which you can smooth to a
example.
[EMMP] Max Engelstein, Anthony Marcuccio, Quinn Maurmann, and Taryn Pritchard, Isoperimetric problems on the sphere and on surfaces with density, New York J. Math. 15 (2009), 97–123. http://www.emis.de/journals/NYJM/j/2009/15-5.html
Frank Morgan, Isoperimetric symmetry breaking: a counterexample to a generalized form of the log-convex density conjecture, Anal. Geom. Metr. Spaces 4 (2016), 314-316.
 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the
Antonio:
Dear Frank,
very nice review!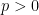 for the result of Dahlberg et al.
for the result of Dahlberg et al.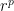 ).
).
I think you forgot indicating
(discs through the origin are isoperimetric for density
Best,
Antonio
Thanks, fixed. —Frank
18 February 2011, 8:10 amFrank Morgan » Blog Archive » Density exp±r^a:
[…] interesting class of densities for the isoperimetric problem on Rn is exp±ra. The Log-convex Density Conjecture says that spheres about the origin are isoperimetric if and only if 0≤a≤1 with the minus sign […]
21 February 2011, 4:19 pmFrank Morgan » Blog Archive » Isoperimetric Regions with Density:
[…] R2 with density exp(r2), where classical isoperimetric regions are balls about the origin, among regions with density the isoperimetric optimum for every area is the same disc of radius r ~ […]
24 April 2013, 6:00 amFrank Morgan » Blog Archive » Symmetrization:
[…] Note: Steiner and Schwarz symmetrization fail for non-product densities f on Rn. […]
10 September 2013, 8:14 am