Archive for the ‘Math’ Category.
23rd May 2011, 12:21 am
Riddle 1. If you take a cab to the airport at 3:30 am Sunday morning and you get stuck in a traffic jam, where are you?
Answer. In Manila.
Riddle 2. If you take a direct flight from Manila to Detroit, why do you go through security twice? Continue reading ‘Riddling Back to the US’ »
17th May 2011, 09:21 pm
From the moment you get off the plane, you experience the friendliness of the Filipinos. My host Fidel Nemenzo, President of the South-East Asia Mathematical Association and famous student revolutionary against the Marcos dictatorship, I have found to be also an extraordinary teacher and gourmet cook. Malou Lopez, who worked briefly as Williams College Mathematics Department secretary, arranged a splendid lunch for me with the College of Business Administration.
6th May 2011, 09:12 pm
Herbert Federer, one of the founders of geometric measure theory, was a good friend to me. I met him at my first conference, at Park City, Utah, as a graduate student in 1977. My advisor at Princeton, Fred Almgren, was one of his graduate students and had shared fond memories with us students.
The first talk was completely incomprehensible to me, and I was afraid I would be exposed as a mathematical ignoramus. I hoped somehow to sneak quietly out of the lecture room. As we filed out in twos from opposite sides of the room, I was alarmed to find myself paired with the famous Federer. As he turned to me I prepared for the inevitable humiliation. His words: “I didn’t understand a word of that talk. Let’s go for a walk and you can tell me about your thesis.” From that day I found him a good friend. Continue reading ‘Herbert Federer’ »
3rd May 2011, 09:55 pm
Daniel Quillen, who won the Field Medal in 1978, passed on April 30, 2011. As a young Moore Instructor at MIT, I went to his office to ask him for advice on doing research. He said that to read a paper and learn something new, he had to find a way to get at it. He said it often lay on his desk for a week or two before he could find a way to approach it.
Incidentally, he was an excellent lecturer. His blackboards, including his writing, were works of art.
Category:
Math |
Comments Off on Daniel Quillen
1st May 2011, 05:11 am
Mathematics and academics are respected and popular in Singapore. Supermarket check-out counters feature math “revision papers” (apparently Singaporean for “review guides”; first photo) and top students do product endorsements on billboards (second photo).


Photos courtesy Helmer Aslaksen, my gracious host.
Category:
Math |
Comments Off on Finding Math Prestigious in Singapore
4th April 2011, 01:16 pm
When friends hear that I’m on a math visit to Pakistan, they often say something about safety. Actually, despite heightened security, I’ve felt completely safe and at home here. The culminating experience was setting up my computer well before talks at QAU, NUST, and GCU* and finding I could leave it unattended, rarely the case in the US or anywhere else.
Incidentally, as of 2008-09, 46% of undergraduates in Pakistan are women, up from 37% in 2001-02. During this period total enrollment has more than doubled. Similarly 31% of PhD students are women, up from 20%.
*See the article by Loring Tu on the GCU “Abdus Salam School of Mathematical Sciences in Pakistan” in the August 2011 Notices of the American Mathematical Society.
4th April 2011, 09:15 am
The most important lemma of regularity for an m-dimensional area-minimizing surface S in Rn is the monotonicity of the mass ratio about a point p of S, i.e., the ratio of the area inside an n-ball about p of radius r to the volume of an m-ball of radius r [FF, Thm. 9.13 and proof], [M, 9.3]. Here in Lahore, Pakistan, at the Abdus Salam School of Mathematical Sciences, Rein Zeinstra told me that such monotonicity generalizes a similar result by Lelong [L] for complex analytic varieties (which are area minimizing). Similarly, the compactness theorem of geometric measure theory generalizes a later such result for complex analytic varieties. See a Math Review by Stoll.
[FF] Herbert Federer and Wendell H. Fleming, Normal and integral currents, Ann. of Math. 72 (1960), 458-520.
[L] Pierre Lelong, Propriétés métriques des variétés analytiques complexes définies par une équation, Ann. Sci. École Norm. Sup. 67 (1950), 393–419.
[M] Frank Morgan, Geometric Measure Theory: a Beginner’s Guide, Academic Press, 4th ed., 2009.
Category:
Math |
Comments Off on Monotoncity from Lelong to Federer-Fleming
29th March 2011, 01:21 pm
In Section 3 of his article on “Crystals, Proteins, Stability and Isoperimetry” in the April 2011 Bulletin of the American Mathematical Society, Misha Gromov suggests that a complex subvariety S of a Kähler manifold X minimizes a curvature energy defined as the volume of the unit tangent bundle S′ in the Grassmannian bundle X′ of X. Here we note that this holds for complex curves in the following sense:
Proposition. Let S be a complex curve in Cn. Then compact portions of S minimize curvature energy among surfaces (rectifiable currents) with the same boundary and the same tangent planes (almost everywhere) along the boundary.
Proof. The Grassmannian bundle is a Kähler manifold, and S′ is a complex curve, hence volume minimizing for given homology class and boundary, which corresponds to boundary and tangent planes along the boundary for S.
For example {x2=y3} in C2, with that interesting singularity at the origin. I don’t know what condition on a more general Kähler manifold X guarantees that X′ is a Kähler manifold.
Incidentally, there is a recent arXiv post on “Willmore minimizers with prescribed isoperimetric ratio” by Johannes Schygulla.
Category:
Math |
Comments Off on Complex Curves Minimize Curvature
23rd March 2011, 08:37 am
Barbosa and do Carmo [BdC] proved that a compact, stable, oriented, immersed constant-mean-curvature surface S in R3 is umbilic and hence a round sphere. The proof works for hypersurfaces in Rn as well. The proof was simplified by Wente [W], generalized to cones by Morgan and Ritoré [MR], incorrectly generalized to warped products by Montiel [M], and generalized to smooth elliptic integrands by Palmer [P]. Tashiro [T] generalized the fact that umbilic hypersurfaces are round. Locally constant normal variations show that stable implies connected.
Here we give a streamlined version of the proof without passing through the Minkowski formulae. Continue reading ‘Stable Immersions Round’ »
Category:
Math |
Comments Off on Stable Immersions Round
22nd March 2011, 05:37 pm
Guest post by Dr. Doug Corey, Department of Mathematics Education, BYU
Can you calculate the speed of light in water using only a ruler, a laser pointer, and a cup of water topped with plastic wrap (or a piece of an overhead transparency)? OK, you may need a little calculus as well, or if you are really clever you can do it with just trigonometry.
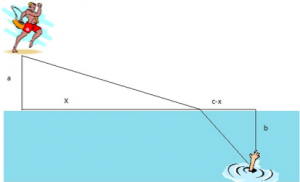 Continue reading ‘The Speed of Light in Water’ »
Continue reading ‘The Speed of Light in Water’ »



 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the