Frank Morgan

Guest post by Dr. Doug Corey, Department of Mathematics Education, BYU

Can you calculate the speed of light in water using only a ruler, a laser pointer, and a cup of water topped with plastic wrap (or a piece of an overhead transparency)? OK, you may need a little calculus as well, or if you are really clever you can do it with just trigonometry.

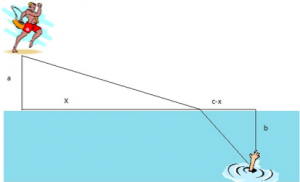I teach a lot of calculus and love finding real and really fun problems. I made up a lab where we use optimization to find the speed of light in water (as a fraction of the speed of light in air) using only the tools above. As a lead-up to the lab we do a variation of the often used lifeguard problem. In this problem a lifeguard on the beach has to run to the beach and then swim to save a struggling swimmer as in the picture below. The distances are given (with c the vertical distance between the lifeguard and the swimmer). What makes this problem interesting is that the lifeguard runs faster than he can swim. Our lifeguard can swim only one-third as fast as he can run on the sandy beach.  The question is at what point should the lifeguard run to on the beach before he starts to swim to the struggling swimmer to get there in the shortest amount of time?  The time to get to the swimmer is given by

,

which comes from the Pythagorean Theorem to get the two distances and dividing by the rate of the lifeguard. I have used s for the speed of the lifeguard running on the beach so the speed of the lifeguard swimming in the water is one-third that, s/3. The two parts of the function T(x) are distances divided by a rate, which of course results in the time it takes for the lifeguard to get to the swimmer (time=distance/rate). From here the answer to the lifeguard problem is easily found by solving the equation T′(x)=0 for x.

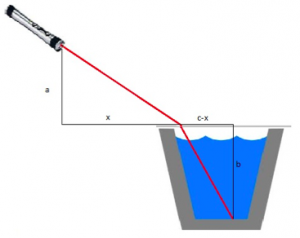
Below is a diagram of the situation that happens when light travels from air, into water. The light (or laser in this case) is “bent” in a similar way that the optimal path of the lifeguard is “bent.” (There is a small flaw in the diagram because,  of course, light will not bend until it actually hits the water, not just the top of the cup). One way to make sense of this bending is that light always takes the quickest path to get from one point to another, just as the lifeguard tries to do. The problem of calculating the speed of light in water is the same as the lifeguard problem except we will know the optimal point of entry but we don’t know speed of light in water (as a fraction of the speed of light in air). I have my students set up the situation like the diagram below and measure the four distances a,b, c, and x with a ruler. It is easiest to measure if you have a stable object, like a book or a ruler standing up on the table, to hold the laser pointer against so it doesn’t move around. We set up the same function T(x) as we did with the lifeguard problem with our measured values of a,b, and c but instead of s and  (s/3) as the rate in water we substitute s and rs, or you can use 1 and r because it is only the ratio of the speeds that matters. The equation T′(x)=0  has two unknowns, x and r, but because light always takes the quickest path we know that the ruler-measured value for x is a solution to this equation. Substituting in the value for x and solving for r gives an estimate for the speed of light in water.

If the measurements are taken carefully then we often get estimates between .76 and .78. The true value is .75; that is, the speed of light in water is three quarters of the speed of light in air. This method usually produces over estimates, and if you have any insight into why this might be I would love to hear them.  As for the trigonometric approach, I will let you try to figure it out.