Frank Morgan

An interesting class of densities for the isoperimetric problem on Rⁿ is exp(±r^a). The Log-convex Density Conjecture says that spheres about the origin are isoperimetric if and only if 0≤a≤1 with the minus sign or a ≥ 1 with the plus sign, known for a=2 [Borell; see Rosales et al.] and in R² for a≥2 [Maurmann-Morgan]. Henceforth we’ll focus on R². Continue reading ‘Density exp(±r^a)’ »

I got this news from my friend Reza Sarhangi:
Fields Medalist William Thurston will be a plenary speaker at
BRIDGES 2011: Mathematics, Music, Art, Architecture, Culture
University of Coimbra, Portugal, July 27-31, 2011 Continue reading ‘Thurston to Speak at Bridges Conference in July’ »

Rodrigo Banuelos suggested studying the isoperimetric problem for the radial density 1/(1+r²) corresponding to the square root of the Laplacian just as the most important Gaussian density corresponds to the Laplacian itself.

Proposition. Consider Rⁿ with density 1/(1+r²). For n > 1 minimizers of perimeter for given volume do not exist: the perimeter can go to zero as the region goes off to infinity. On the line, for more than half the volume the minimizer is a ball about the origin, for less than half, the complement, for exactly half, the ball, its complement, or a half-line. In particular, balls about the origin are minimizing while stable, up to radius 1, with (log density)” = 2(x²-1)/(x²+1)². Continue reading ‘Density 1/(1+r^2)’ »

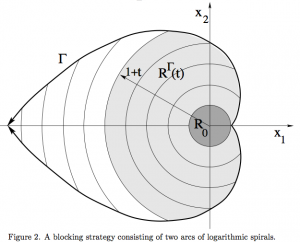
Prof. Alberto Bressan at Penn State offers a $500 prize for proving the optimal firebreak to isolate a forest fire that begins in the unit disc. I guess the answer is the heart shape of his Figure 2, the upper half of which he knows to be optimal in the half-plane. (Happy Valentine’s Day.)

Note added February 7, 2011. The announced counterexample was wrong. It does not satisfy the hypothesis of the conjecture. Geodesic circles about the origin in Enneper’s surface are unstable.

The proposed generalization of the Log-convex Density Conjecture to separate densities for volume and perimeter fell at the centennial congress of the Royal Spanish Mathematical Society.  The counterexample—Enneper’s Surface—emerged from discussions with participants in the Geometric Analysis session, notably Manuel Ritoré, Antonio Ros, Cesar Rosales, and Antonio Cañete.

Another way of stating the hypothesis for a single density for volume and perimeter is that the generalized Ricci curvature, equal to the Riemannian Ricci curvature (0 for Euclidean space) minus the Hessian of the log of the density be nonpositive. General separate perimeter and volume densities are equivalent to a conformal change of metric together with a density. The counterexample, Enneper’s Surface, is conformally the plane (with unit density) and intrinsically a surface of revolution. As a minimal surface, it has negative curvature. Since the curvature is negative at the origin and approaches 0 at infinity, small balls about the origin have larger perimeter than small balls near infinity, and the generalized conjecture fails.

Preliminary announcement February 4, 2011.