Frank Morgan

In Section 3 of his article on “Crystals, Proteins, Stability and Isoperimetry” in the April 2011 Bulletin of the American Mathematical Society, Misha Gromov suggests that a complex subvariety S of a Kähler manifold X minimizes a curvature energy defined as the volume of the unit tangent bundle S′ in the Grassmannian bundle X′ of X. Here we note that this holds for complex curves in the following sense:

Proposition. Let S be a complex curve in Cⁿ. Then compact portions of S minimize curvature energy among surfaces (rectifiable currents) with the same boundary and the same tangent planes (almost everywhere) along the boundary.

Proof. The Grassmannian bundle is a Kähler manifold, and S′ is a complex curve, hence volume minimizing for given homology class and boundary, which corresponds to boundary and tangent planes along the boundary for S.

For example {x²=y³} in C², with that interesting singularity at the origin. I don’t know what condition on a more general Kähler manifold X guarantees that X′ is a Kähler manifold.

Incidentally, there is a recent arXiv post on “Willmore minimizers with prescribed isoperimetric ratio” by Johannes Schygulla.

Barbosa and do Carmo [BdC] proved that a compact, stable, oriented, immersed constant-mean-curvature surface S in R³ is umbilic and hence a round sphere. The proof works for hypersurfaces in Rⁿ as well. The proof was simplified by Wente [W], generalized to cones by Morgan and Ritoré [MR], incorrectly generalized to warped products by Montiel [M], and generalized to smooth elliptic integrands by Palmer [P]. Tashiro [T] generalized the fact that umbilic hypersurfaces are round. Locally constant normal variations show that stable implies connected.

Here we give a streamlined version of the proof without passing through the Minkowski formulae. Continue reading ‘Stable Immersions Round’ »

Guest post by Dr. Doug Corey, Department of Mathematics Education, BYU

Can you calculate the speed of light in water using only a ruler, a laser pointer, and a cup of water topped with plastic wrap (or a piece of an overhead transparency)? OK, you may need a little calculus as well, or if you are really clever you can do it with just trigonometry.

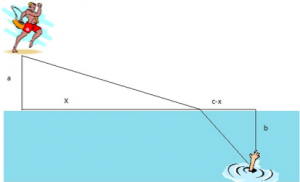Continue reading ‘The Speed of Light in Water’ »

[“Soap Bubbles and Mathematics,” written for the Spanish Math Carnival]

¿Por qué son las pompas de jabón tan perfectamente redondas?

Continue reading ‘Pompas de Jabón y las Matemáticas’ »