Baserunner’s Optimal Path
Note added 13 June 2017: see a video featuring Prof. Johnson at the NESN Clubhouse.
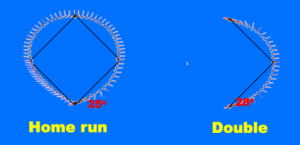
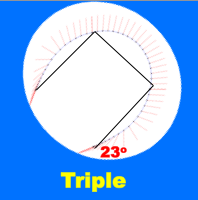
In his senior colloquium last fall advised by Frank Morgan, Davide Carozza ’09 investigated the fastest path around the bases in baseball, assuming a bound of say 10 ft/sec2 on acceleration/deceleration. Following the baseline, stopping at each base, takes about 22.2 seconds. The standard recommended “banana” path follows the baseline maybe halfway to first base and then veers a bit to the right to come at first base from a better angle to continue towards second. That cannot be ideal. It would have been better to start at an angle to the right to head directly to an outer point on the banana path. Davide found that a circular path at 17.8 seconds is roughly 20% faster than following the baseline at 22.2 seconds. Stewart Johnson then computed the following optimal path at 16.7 seconds. The record time according to Guiness is 13.3 seconds, set by Evar Swanson in 1932 (with larger acceleration than our assumed 10 ft/sec2).

Is it legal to run so far outside the base path? The relevant official rule of Baseball says:
7.08 Any runner is out when—
(a) (1) He runs more than three feet away from his baseline to avoid being tagged unless his action is to avoid interference with a fielder fielding a batted ball. A runner’ s baseline is established when the tag attempt occurs and is a straight line from the runner to the base he is attempting to reach safely.
The rule just says that after a tag attempt the runner cannot deviate more than three feet from a straight line from that point. The rule doesn’t apply until the slugger is almost home, when our fastest path is nearly straight. So our path is legal.
Our model is, of course, an oversimplified one, since it assumes that maximum deceleration equals maximum acceleration and that maximum acceleration remains possible at high speeds, leading to a final speed coming into home of about 42 ft/sec, faster than the highest recorded human speed of 40 ft/sec by Usain Bolt.
For more, see the web version of our “Baserunner’s Optimal Path,” published online in The Mathematical Intelligencer, November, 2009, Johnson’s interview on NPR, the citation in Rob Neyer’s Monday Mendozas on how to get more triples in baseball, the Berkshire Eagle (front page, see below), the Williams College news release, “World Series Take Notice,” Live Science, Science News, Math Goes Pop, our article in Collegiate Baseball Newspaper, 12 Feb. 2010, my Huffington Post post, and for more on the computation “Computing Minimum Time Paths With Bounded Acceleration” by Johnson.
Davide Carozza, Stewart Johnson, and Frank Morgan


 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the
Nick:
Am I missing something? Your optimal path and some assumptions about the acceleration of the runner yield a run which is both a) slower than the fastest recorded base run time and b) attains a speed which surpasses recorded human speed? Is this because in real life people slide to a halt rather faster than they accelerate?
5 March 2009, 6:00 pmIvan:
Interesting result. One question – which of you have attempted physical evidence of the superiority of this path? I think a faculty baseball game (math vs. physics) is in order, and this is your secret weapon!
6 March 2009, 9:52 amStewart Johnson:
A real runner probably has greater forward acceleration than our model presumes, hence jumping up to the higher speeds in less time. Forward acceleration is significant in going from home to first. After that, lateral acceleration dominates.
As a real runner approaches maximum speed, more energy goes into sustaining the mechanical effort, less to none available for continued acceleration. Hence the overestimation in the final sprint to home.
6 March 2009, 10:35 amThomas:
I would say that the next step would be to see if you can incorporate maximum velocity into your calculations, if at all possible.
As a baseball player, I can offer the justification behind the standard “banana” path. Calling home plate both n=0 and n=4, it should be noted that if base n is assumed to be safe but base n 1 is in doubt, the banana path is probably more efficient. At the time the decision is made whether or not to advance to base n 1, the runner wants to be as close to base n 1 as possible. This advantage is worth getting to base n more slowly.
6 March 2009, 2:28 pm09das:
Maurice Green is, in fact, already in history books. The top instantaneous speed was achieved by Usain Bolt (12.2 m/s) in Beijing 2008 Olympics 100m final.
http://speedendurance.com/2008/08/22/usain-bolt-100m-10-meter-splits-and-speed-endurance/
Thanks, we’ve edited the entry — FM.
6 March 2009, 4:24 pmTom:
Are you sure this basepath is legal? It seems to veer widely of the striped box that runs from 45 feet between home and first and first. Granted, umpires call this about as consistently as the strike zone but it is in the rule book, isn’t it?
28 September 2009, 6:01 pmBloody Sox Laundry, 9/29/09 - Improving the Game and the Team:
[…] Baserunner’s Optimal Path – Frank Morgan […]
29 September 2009, 6:05 amSweet Uncle Lou’s Friday Roundup: The “Touch Your Helmet Not Once, Not Twice, But Thrice for a Curveball” Edition | Hire Jim Essian:
[…] says geeks and jocks can’t get along? As long as the geeks tell the jocks how to run the bases, it’s a perfect match. (HT: […]
2 October 2009, 11:08 amFrank Morgan:
Front page story in the Berkshire Eagle and North Adams Transcript Friday, October 2, 2009. Front page and figure inside.
3 October 2009, 11:20 amReadings: Big Machines, Harvard, Births, China, Facebook, Baserunners, etc. | Venture Capital Bloggers Network:
[…] Baserunner’s Optimal Path (Source) […]
7 April 2010, 4:36 amThe 27th Annual Anja S. Greer Conference on Mathematics, Science, & Technology | FracTad's Fractopia:
[…] Morgan of Williams College, about how one of his students’ projects was to calculate the optimal path a baserunner should take around a baseball diamond. It garnered lots of publicity and generated further research. He also showcased some of his […]
28 June 2011, 11:02 pmMitch:
Frank: great work. Question: have you given any thought to this issue as it applies to girls’/women’s fastpitch softball? (Presumably slower athletes, and 60 foot bases.) I would really be interested in your ideas. Thanks.
Interestingly enough, the best path is exactly the same regardless of the size of the diamond on the maximal acceleration of the baserunners. (Slower runners should follow exactly the same path, although it will take them longer than faster runners.)—fm
27 July 2011, 9:53 amMitch:
Frank: Thanks for the info. Interestingly, my daughter was at a softball tournament this past weekend that included some “skills” competitions after opening ceremonies. She competed in the home-to-home running (she placed 3rd, but she’s only a soon-to-be 6th grader competing against soon-to-be 8th graders, so I’ll take it!) A lot of the “faster” girls (including my daughter) took a wide turn around 3rd base, taking them maybe 8 or 10 feet out of the baseline. The girl who won it (one of my daughter’s teammates) was only 3 or 4 feet out of the baseline after she made her turn at 3rd. And she won the competition by almost a full second (low 12’s—only the very fastest Division I softballers can break 11). This was what started me on my internet reseach that lead to your paper. And the experience from this past weekend seems to—at least anecdotally—support your research. I think the key is having the presence of mind to head off toward the 1st base dugout or coach’s box as soon as possible out of the batter’s box. Thanks again.
27 July 2011, 1:32 pmmpls routing protocol:
the points you are trying to make seem conflicting to me if the fastest way around your asssuming is faster than the average human but the fastest time was set almost 80 years ago which is faster than yours they seem to conflict have you trialled it out and done a practical test or is it all theory?
Faster just in final sprint. Mostly theory, some testing.—fm
11 May 2013, 11:11 pmFrank Morgan:
On Jul 19, 2014, at 7:11 AM, [email protected] wrote:
…first to third should be symmetrical, just like home to second. Second to home should bulge out between second and third.
From: “Lawson, Andrew D”
Date: Tue, 22 Jul 2014 06:49:22 -0500
Thank you Frank. That makes a lot of sense to me.
For most of my career, until 2 outs, the base runner at second base was taught to take his lead in the base line. This last season, we taught our players to always take their lead at second base ~10 feet deep (depending on player’s speed and strength), outside of the base line. Our thought was to simply start the base runner on the bulging arc that we are talking about. We were much more efficient scoring base runners at second base this season, and I think this small adjustment played a big role.
22 July 2014, 8:06 ambchiem:
Hi everyone,
Reading this very interesting article, I asked myself some questions about the mathematical aspects behind this optimization problem. What is the objective function? I mean, what do we want to optimize? Total time, max acceleration…?
Which constraints are there in this problem, aside from the max acceleration and the 3 feet rule?
The problem is, I really don’t understand how to modelize this problem…
Minimize time given bound on acceleration. — fm
16 October 2015, 9:01 am