The SMALL REU
I advised groups as part of Williams College’s SMALL REU in 2017, 2018, 2020, and 2021. Check out the research page for our publications!

SMALL Tropical Geometry 2017 at the Young Mathematician’s Conference in Columbus, OH (Andrew Scharf ’18, Sifan Jiang, Desmond Coles, Neelav Dutta, RM)

SMALL Tropical Geometry 2018 at Mathfest in Denver, CO (Teresa Yu ’20, Julie Yuan, Franny Dean ’19, RM, Ivan Aidun, Sammy Rosofsky ’19)
SMALL Tropical and Algebraic Geometry 2020 on Zoom (Robin Huang ’21, Liza Jacoby ’22, Marino Echavarria, Ben Weber ’21, Raluca Vlad, Max Everett ’21)

SMALL 2021 Chip-Firing Games in the Frank Morgan Library (Jason Meintjes ’22, Liz Ostemeyer ‘22.5, Lizzie Ferguson ’22, Lisa Cenek, Shefali Ramakrishna, Eyobel Gebre ’22, Cassandra Marcussen)
Thesis students
I have advised eight senior honors theses at Williams College, as well as a minithesis:
- Madeleine Elyze ’18: On higher distance commuting matrices
- Andrew Scharf ’18: Intersections of tropical surfaces
- Jian Lu ’19: Time complexities in max-linear systems
- Max Everett ’21: Multiplicity-free gonality on graphs
- Robin Hung ’21: The tropical Three Conics Theorem
- Ben Weber ’21: On gonality-related graph parameters
- Jason Meintjes ’22: Tropical Brianchon’s Theorem
- Lucas Tolley ’22: Higher order gonalities of graphs
- Robin Eagleton ‘22.5: Characterizing graphs of small scramble number (minithesis)
Class projects
Most of my upper level classes include a final project. Here are a few of those!
Nullstellenfont (by Ben Logsdon ’20 and Anya Michaelsen ’19, for Math 487: Computational Algebraic Geometry in Spring 2019)
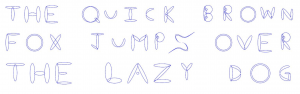
Algebraic geometry studies varieties, which are shapes defined by polynomial equations. For instance, polynomials in two variables define curves in the plane. For their final project, Ben and Anya designed a typographical font called “Nullstellensatz”, which lets you represent any string of letters using a single polynomial equation! For instance, here’s a polynomial defining a curve that looks like my name. If you’d like to make your own, you can download their code here.
Chip-firing tool (by Markus Feng ’21 for Math 334: Graph Theory in Spring 2019)
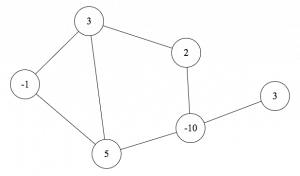
Chip-firing games on graphs involve placing an integer number of chips on the vertices of the graph, and then moving those chips around by “firing” vertices, which makes them donate a chip to each neighbor. For his final project in my Graph Theory class, Markus designed a great tool for drawing graphs and then performing chip-firing moves on them.
This one isn’t really a final project, but the students in Math 474: Tropical Geometry put together a gallery of tropical curves. Check it out here!