My research is broadly in the realm of computational algebraic geometry, with particular focus on tropical and non-Archimedean geometry.  Here are my preprints and publications, with some pictures and brief descriptions.  Authors who were undergrads when the research was undertaken are listed in bold.

Preprints

(32) “The gonality of chess graphs” with Nila Cibu, Kexin Ding, Steven DiSilvio, Sasha Kononova, Chan Lee, and Krish Singal. (arXiv)

A chess graph encodes the ways that a chess piece can move around on a rectangular chess board.  We study chip-firing games on these graphs, and find upper and lower bounds on the gonality for king’s, bishop’s, and knight’s graphs.  (This work was part of the 2023 SMALL REU.)

(31) “On the size and complexity of scrambles” with Seamus Connor, Steven DiSilvio, Sasha Kononova, and Krish Singal.  (arXiv)

A scramble of a graph is a collection of connected subgraphs (called “eggs”), and we measure the order of scramble by how hard it is to hit every egg, and how hard it is to separate some pair of eggs.  We show that in order to build a scramble on maximum order, sometimes we need exponentially many eggs!  (This work was part of the 2023 SMALL REU.)

(30) “The gonality of queen’s graphs”, with Noah Speeter.  (arXiv)

A queen’s graph encodes the ways that a queen can move around on a rectangular chess board.  We study chip-firing games on these graphs, and show that finding divisors of positive rank and minimum degree is intimately related to finding maximum collections of non-attacking queens.

(29) “Scramble number and tree-cut decompositions” with Lisa Cenek, Lizzie Ferguson, Eyobel Gebre, Cassandra Marcussen, Jason Meintjes, Liz Ostermeyer, Shefali Ramakrishna, and Ben Weber. (arXiv)

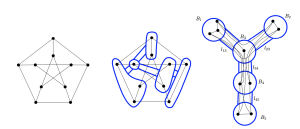
A tree-cut decomposition takes a graph and puts it inside of a tree.  We introduce a new invariant, called the screewidth of a graph, which measures how “full” the tree needs to be.  We relate this new invariant to scramble number and to graph gonality. (This work was part of the 2021 SMALL REU.)

(28) “Computing higher graph gonality is hard”, with Lucas Tolley. (arXiv)

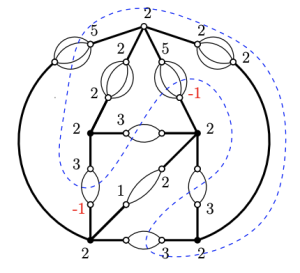
The r-th gonality of a graph is the minimum number of chips we need so that we can place r of them wherever we would like, using chip-firing moves.  We prove that it’s hard (more precisely, NP-hard) to compute r-th gonality for a graph, and that the same is true for many related problems.

(27) “Bounds on higher graph gonality”, with Lisa Cenek, Lizzie Ferguson, Eyobel Gebre, Cassandra Marcussen, Jason Meintjes, Liz Ostermeyer, and Shefali Ramakrishna. (arXiv)

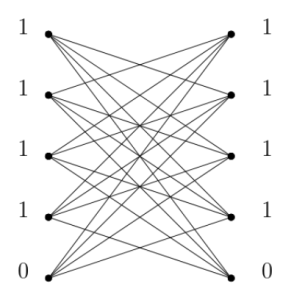
The r-th gonality of a graph is the minimum number of chips we need so that we can place r of them wherever we would like, using chip-firing moves.  We prove some new upper and lower bounds on r-th gonality. (This work was part of the 2021 SMALL REU.)

Publications

(26) “Uniform scrambles on graphs”, with Lisa Cenek, Lizzie Ferguson, Eyobel Gebre, Cassandra Marcussen, Jason Meintjes, Liz Ostermeyer, and Shefali Ramakrishna.  Australasian Journal of Combinatorics 87 (2023), 129–147. (arXiv)

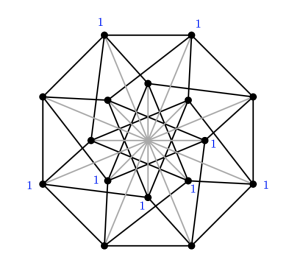
A scramble is a collection of connected subgraphs of a graph.  We study scrambles where every subgraph has the same number of vertices, and use that to study chip-firing games.  (This work was part of the 2021 SMALL REU.)

(25) “Multiplicity-free gonality  on graphs”, with Franny Dean and Max Everett. The Electronic Journal of Graph Theory and Applications 11 (2023), no. 2, 357–380.  (arXiv)

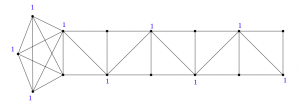
The gonality of a graph measures how few chips we need so that we can move the chips anywhere using chip-firing moves.  We introduce multiplicity-free gonality, which asks how few chips we need if they’re all placed on different vertices.

(24) “Graphs of scramble number two” with Robin Eagleton. Discrete Mathematics,
Volume 346, Issue 10, 2023. (arXiv)

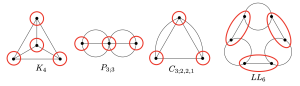
The scramble number of a graph is a new invariant that helps us study chip-firing games.  In this paper, we classify all graphs of scramble number two.

(23) “Iterated and mixed discriminants”, with Alicia Dickenstein and Sandra di Rocco. J. Comb. Algebra 7 (2023), no. 1, 45–81.  (arXiv)

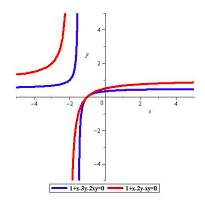
Discriminants tell us when polynomials have solutions of higher multiplicity. In this paper we study when certain discriminants can be computing by taking discriminants of other discriminants.

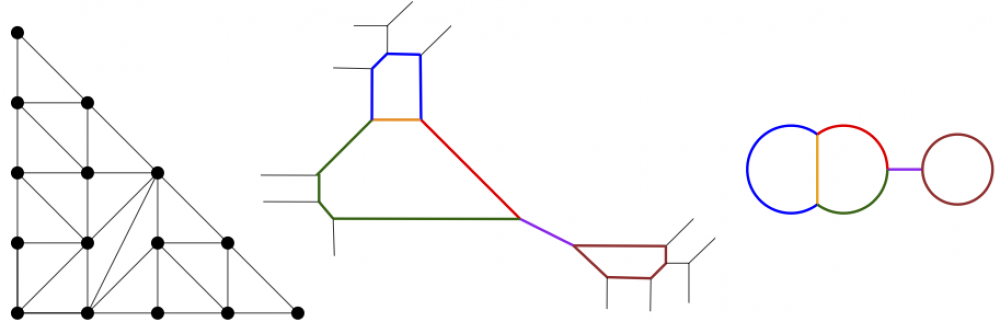
(22) “Tropically planar graphs”, with Desmond Coles, Neelav Dutta, Sifan Jiang, and Andrew Scharf, Collect. Math. 74 (2023), no. 1, 27–60 (arXiv; supplemental material)

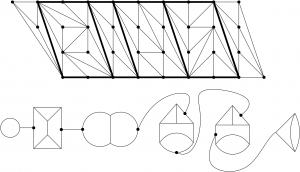
Tropically planar graphs appear in smooth tropical plane curves, and are dual to triangulations of polygons.  We compute how many graphs are tropically planar up to genus 7, and give upper and lower bounds on their number in general. (This work was part of the 2017 SMALL REU.)

(21) “On the scramble number of graphs”, with Marino Echavarria, Max Everett, Robin Huang, Liza Jacoby, and Ben Weber, Discrete Appl. Math. 310 (2022), 43–59. (arXiv)

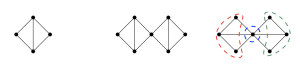
The scramble number of a graph is a new invariant that helps us study chip-firing games.  We prove lots of results about scramble number, including that it’s NP-hard to compute!  (This work was part of the 2020 SMALL REU.)

(20) “Moduli dimensions of lattice polygons”, with Marino Echavarria, Max Everett, Robin Huang, Liza Jacoby, Ayush K. Tewari, Raluca Vlad, and Ben Weber, The Journal of Algebraic Combinatorics 55 (2022), no. 2, 559-589. (arXiv)

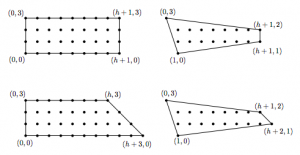
Given a lattice polygon, we can ask: how many degrees of freedom d are there in constructing a tropical (or algebraic!) curve with that Newton polygon?  We determine all possible values of d for lattice polygons.  (This work was part of the 2020 SMALL REU.)

(19) “The moduli space of tropical curves with fixed Newton polygon”, with Desmond Coles, Neelav Dutta, Sifan Jiang, and Andrew Scharf, Advances in Geometry 22 (2022), no. 1, 49-68. (arXiv)

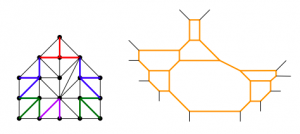
Tropical plane curves contain graphs with lengths assigned to their edges.  We show how to find the number of degrees of freedom we have in choosing those lengths, either for a single triangulation or for a whole  polygon.  (This work was part of the 2017 SMALL REU.)

(18) “Gonality sequences of graphs”, with Ivan Aidun, Franny Dean, Teresa Yu, and Julie Yuan, SIAM Journal on Discrete Mathematics 35 (2021), no. 2, 814–839.  (arXiv)

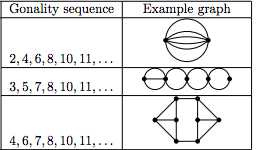
For any graph, we can study an infinite family of chip-firing games on that graph called the gonality games. The gonality sequence of a graph is a list of numbers that measure how hard it is to win those games.  We determine what gonality sequences look like for small graphs, how gonality sequences can start, and how to compute them. (This work was part of the 2018 SMALL REU.)

(17) “Prism graphs in tropical plane curves”, with Liza Jacoby and Ben Weber, Involve, a Journal in Mathematics,14-3 (2021), 495–510. (arXiv)

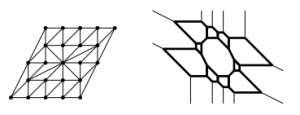
The tropical plane curve pictured above has a prism graph with 11 bounded regions.   We prove that there exists no larger prism in a tropical plane curve.  (This work was part of the 2020 SMALL REU.)

(16) “On the gonality of Cartesian products of graphs”, with Ivan Aidun, Electronic Journal of Combinatorics 27 (2020), no. 4, Paper No. 4.52, 35 pp.  (arXiv)

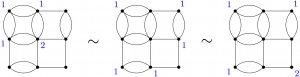
If you know how to win a chip-firing game on two graphs G and H, then there’s a strategy to win on their product.  We study when this strategy is optimal, and when there are even better ones.  (This work was part of the 2018 SMALL REU.)

(15) “Higher-distance commuting varieties”, with Madeleine Elyze, Alexander Guterman, and Klemen Sivic, Linear and Multilinear Algebra 70 (2022), no. 17, 3248–3270.  (arXiv)

 

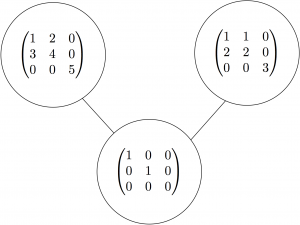
Two matrices A and B commute if AB=BA.  If two matrices don’t commute, they still might commute with a common non-scalar matrix.  We show that this condition is determined by polynomial equations.  (This includes thesis work by Madeleine Elyze, Williams ’18.)

(14) “Convex lattice polygons with all lattice points visible”, with Ayush K. Tewari, Discrete Mathematics 344 (2021), no. 1, Paper No. 112161, 19 pp.  (arXiv)

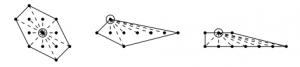
The three polygons above have a circled grid point that can “see” all the other grid points in the polygon.  What can such a polygon look like? We provide a complete answer, and give some cool applications to tropical geometry.

(13)  “Tropical Geometry” (2020). In P. Harris, E. Inkso, & A. Wootton (eds.), A Project-Based Guide to Undergraduate Research in Mathematics: Starting and Sustaining Accessible Undergraduate Research (pp. 63-105).  Birkhäuser Basel. (arXiv)

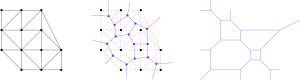
This chapter contains a quick introduction to tropical geometry, and then lots of open problems accessible to undergrads.  Also check out the other chapters from the book!

(12) “Nullstellenfont,” with Ben Logsdon and Anya Michaelsen, Math Horizons, 27:4, 5-7 (2020).

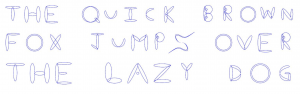
An algebraic plane curve is defined by a polynomial in two variables.  Given any string of text, we can give you a polynomial whose corresponding curve looks like that string.  Try it out on this website!

(11) “Tropical hyperelliptic curves in the plane,” The Journal of Algebraic Combinatorics 53 (2021), no. 2, 369-388.  (arXiv)

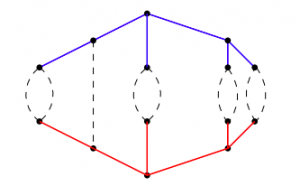
Tropical hyperelliptic curves are graphs that are built out of two copies of a tree glued together.  We show which of these graphs can appear in smooth tropical plane curves.

(10) “Treewidth and gonality of glued grid graphs”, with Ivan Aidun, Franny Dean, Teresa Yu, and Julie Yuan, Discrete Applied Mathematics 279 (2020), 1-11.  (arXiv)

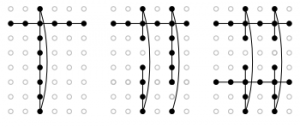
Treewidth measures how close a graph is to being a tree.  We find the treewidth for grid graphs glued along their boundaries, and show how to win chip-firing games on them.  (This work was part of the 2018 SMALL REU.)

(9) “Graphs of gonality three”, with Ivan Aidun, Franny Dean, Teresa Yu, and Julie Yuan, Algebraic Combinatorics, Volume 2 (2019) no. 6 p. 1197-1217. (arXiv)

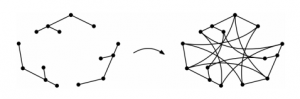
The chip-firing game on a graph lets you place a collection of chips on a graph, which you then move around to eliminate debt placed by an opponent.  In this paper, we study the graphs where you can win the game by starting with just three chips.  (This work was part of the 2018 SMALL REU.)

(8) “The smallest art gallery not guarded by every third vertex”, Geombinatorics 29 (2019), no. 1, 24-32.  (arXiv)

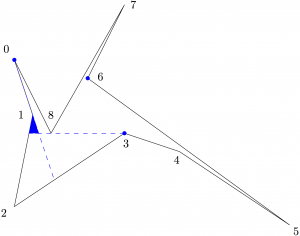
Any polygonal art gallery can be guarded by placing guards on a third of its vertices. But we can’t always place a guard on every third vertex; in this paper, we find the smallest possible example that shows this.

(7) “The tropical commuting variety”, with Ngoc M. Tran, Linear Algebra Appl. 507 (2016), 300–321.  (arXiv)

Two matrices A and B commute if AB=BA.  We study what it means for two matrices to commute tropically, which means that addition is replaced with taking a minimum, and multiplication is replaced with addition.

(6) “Bitangents of tropical plane quartic curves”, with Matt Baker, Yoav Len, Nathan Pflueger, and Qingchun Ren, Mathematische Zeitschrift, 282 (2016), no. 3-4, 1017–1031. (arXiv)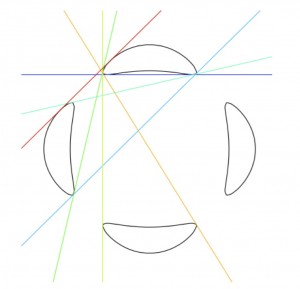 

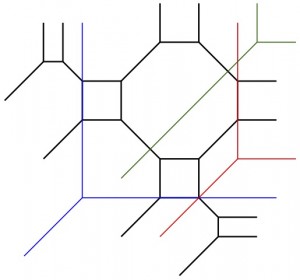
Classically, a smooth plane quartic curve has 28 bitangent lines.  We prove that tropically, such a curve has 7 bitangent lines.

(5) “Moduli of tropical plane curves”, with Sarah Brodsky, Michael Joswig, and Bernd Sturmfels, Research in the Mathematical Sciences, Vol. 2 (2015), 2:4.  (arXiv)

Split a polygon up into triangles, and draw the dual graph.  Which graphs can we see?  We answer this question for polygons with at most 5 lattice points in their interior.

(4) “Tropical images of intersection points”, Collectanea Mathematica, Vol. 66 (2015), Issue 2, 273-283.  (arXiv)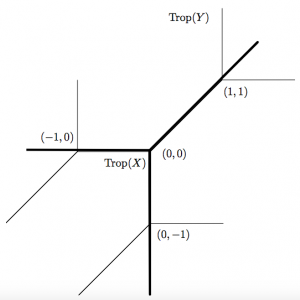

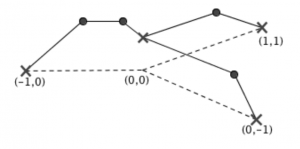
Classical intersection points map to tropical intersection points.  I give a partial answer to the reverse questions:  which tropical intersection points can be lifted to classical intersection points?

(3) “Algorithms for Mumford curves”, with Qingchun Ren, Journal of Symbolic Computation, Vol. 68 (2015), 259-284.  (arXiv)

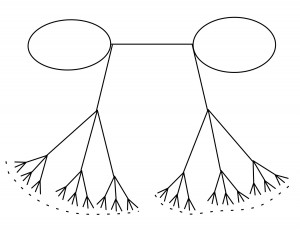
If we let certain groups act on a field, the quotient can be interpreted as an algebraic curve.  We develop algorithms for studying such curves over the field of p-adic numbers.

(2) “An elliptic curve family test of the L-functions Ratios Conjecture”, Duc Khiem Huynh and Steven J. Miller, Journal of Number Theory, Vol. 131 (2011), 1117-1147.  (arXiv)

When studying the zeros of L-functions, it’s helpful to approximate their behavior.  We show that for a family of these functions, a certain approximation is very accurate. (This is based in part on my undergraduate thesis at Williams College with Steve Miller.)

(1) “The spiral index of knots”, Colin Adams, William George, Rachel Hudson, Laura Starkston, Samuel Taylor, and Olga Turanova, Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 149 (2010), Issue 2, 297-315.  (arXiv, PDF)

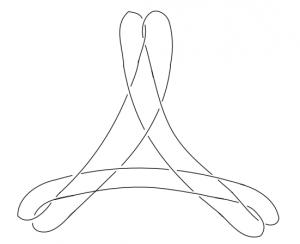
We study spiral projections of knots, which are pictures of knots without any inflection points. (This work came out of Colin Adams’ Knot Theory group in the 2008 SMALL REU.)

Other scholarly works

My dissertation is titled “Tropical and non-Archimedean curves”, written at UC Berkeley with Bernd Sturmfels as my advisor.  You can find a PDF of it here.  It includes material from publications (3) through (7) listed above.