In the summer of 2020, I’ll be leading a group on Tropical and Algebraic Geometry as part of Williams’ SMALL REU. This website contains possible projects the group could work on; in order to apply for this group, you should visit the posting on mathprograms.org. (By the way: there are WAY more projects here than could ever be covered in one REU. Once we figure out what sorts of questions the group members are interested in, we’ll start narrowing down, or figuring out related topics.)
Algebraic geometry is the study of solution sets of polynomial equations, dating back at least to Descartes’ introduction of coordinate systems in the 1500s. Tropical geometry is a new field of mathematics that studies combinatorial, piecewise-linear analogs of the objects in algebraic geometry, often with a view towards understanding the original algebro-geometric objects themselves. For instance, an algebraic curve is a one-dimensional solution set to polynomial equations; and a tropical curve is a union of line segments and rays, embedded in Euclidean space in a balanced way and having the underlying structure of a metric graph. And as an algebraic geometer studies poles and zeros of rational functions on the algebraic curve, a tropical geometry studies configurations of chips on the metric graph, which move around according to chip-firing rules.
The projects for this group will be based in algebraic geometry, tropical geometry, and the interplay between these two fields. Here are a few topics and resources to get a flavor of the sorts of questions we might be thinking about. I’ll frequently refer to this book chapter I wrote, which gives you some background on tropical geometry as well as possible research projects. I’ll also refer to different papers I’ve coauthored, many with undergrads; you can also find all my papers here.
- Tropical theorems from algebraic ones: there are many results from algebraic geometry that also hold in tropical geometry. For instance, Bezout’s theorem tells us how many points two plane curves should intersect in; an almost identical result holds tropically (see Theorem 3). Occasionally we have theorems of a similar flavor, but with a different result: algebraically, a smooth plane curve of degree 4 has 28 bitangent lines; tropically, it has only 7 as shown by me and my coauthors. There are many results from the classical world of algebraic geometry that have not been explored in the tropical setting, and would be perfect for projects for this group (see Project 4 for a few examples).
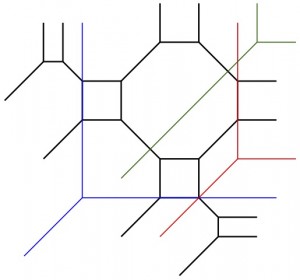
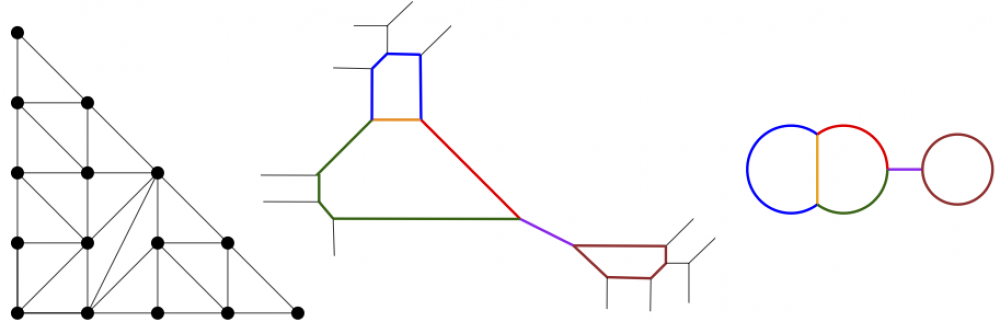
- Properties of embedded tropical curves: A tropical curve in the plane has a beautiful polyhedral structure, and is dual to a subdivision of a related polygon called its Newton polygon. You can read all about this duality in Section 2. Sitting inside such a tropical curve is a graph with lengths on its edges, also known as a metric graph. There are all sorts of questions we can ask: which metric graphs can appear? Or as my SMALL 2017 group asked, how many combinatorial types (forgetting edge lengths) of graphs arise in this way? There are many open questions, like Projects 6-11.
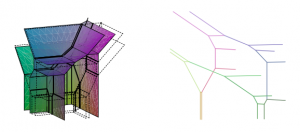
There’s even more information we can hope to get out of the Newton polygons of tropical curves. For instance, we can play chip-firing games (detailed below) on these metric graphs. We might ask a question like: when can we win a chip-firing game on such a graph using only two chips? I proved the answer was if-and-only-if the Newton polygon is especially “thin”, also known as hyperelliptic. What about if we let ourselves use three chips? Or n chips? These questions are very open!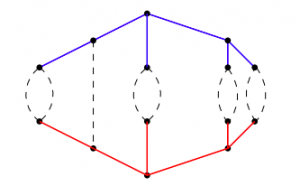
Moving beyond the plane into three-dimensions, even less is known about what tropical curves can look like! There is still a duality theorem, albeit a much more complicated one; see Section 3. Here are a few open questions, drawn from Projects 13-15 in that section: if we intersect tropical surfaces of degrees d and e, what combinatorial properties can their intersection curve look like? (It turns out the simplest nontrivial cases are (d,e)=(1,4) and (d,e)=(2,3); even these cases are open!) If we intersect two tropical surfaces of degree 2, we “expect” to see a tropical elliptic curve; what other intersections are possible? And there’s no need to restrict ourselves to tropical curves or to three-dimensions, either: we can look at tropical surfaces in three-dimensions (Project 12), or in general tropical varieties living in any dimensional space we want!
(image credit: Magnus Vigeland)
- Chip-firing games on graphs: A graph is a collection of nodes (or vertices) connected by edges. We play a chip-firing game on such a graph by placing an integer number of chips on each node of the graph, and then moving them around according to chip-firing moves, where one node donates chips to its neighbors, one along each edge. You can try it out here!
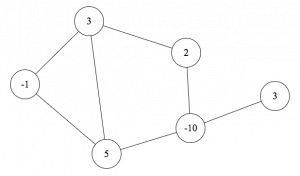The simplest chip-firing game, like the one linked above, has the goal of eliminating all “debt” (or negative numbers of chips) from the graph. A slightly more complicated game is the following: you place k chips on the graph, and then an opponent places -1 chips. You get to chip-fire to try to remove the debt. If you can remove it, you win; if you can’t, then your opponent wins. The gonality of a graph is the smallest k such that you have a winning strategy. This number is hard (in fact, NP-hard!) to compute, but we can hope to try to compute it for certain families of graphs. For instance, my SMALL 2018 group determined the gonality of glued grid graphs; and a SMALL alum and I studied how gonality behaves under taking Cartesian products of graphs. Another strategy is to study graphs with a small gonality, like gonality 2 or (as SMALL 2018 did) gonality 3. There are still loads of open families of graphs whose gonalities are unknown, and would be great to study!
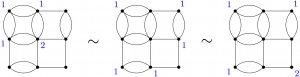We can also look at chip-firing games on metric graphs, which have lengths assigned to their edges, and once again ask about their gonality. This is especially exciting if those metric graphs are coming from tropical curves, as mentioned above with the hyperelliptic results!
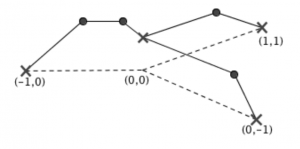
There are also generalizations of the gonality game: for instance, what if the opponent gets to place -2 chips? Or -3? Or more? We can still ask how few chips we need to be guaranteed to win; we call these numbers the second gonality, the third gonality, and so on. There are a few results known about higher gonalities of graphs, but there are still many open questions.
Our group can also study computational questions related to graph gonality. Although it is NP-hard to compute in general, we might hope for certain families of graphs it is not so daunting. For instance, checking if a graph has gonality 2 can be done in quasilinear time! We might try to find similar results for graphs of gonality 2, or for computing the gonality of planar graphs.
- Computational algebraic geometry: Moving to the world of usual algebraic geometry, we study shapes called varieties, which are solution sets to polynomial equations. Given such a shape, we might wonder: how can we find a “nice” set of defining equations? How can we compute properties of the shape from those equations, like dimension? As one example project, a Williams thesis student, a colleague, and I showed that pairs of matrices with bounded commuting distance form a variety. Sadly, our proof of this did not yield particularly nice polynomial equations, and so the dimension of these varieties is currently unknown! Finding a nice set of equations could help us understand these varieties more thoroughly.
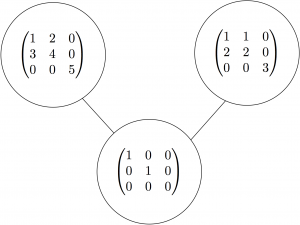Such questions in algebraic geometry may seem far removed from tropical geometry, but it turns out that the two are linked through a process called tropicalization (Section 4). In this way an algebraic variety can be turned into a tropical variety; many properties (such as dimension and degree) are preserved. So to study an algebraic object we may study a more combinatorial tropical one.This spring I will be working with colleagues at the Max Planck Institute at Leipzig’s group on Nonlinear Algebra, we will draw on the work done there as a possible source for REU projects.