12th March 2023, 09:00 pm
 Made the following impossible 3NT playing with Mark Blanchard at the national Lebhar IMP Pairs in New Orleans March 12, 2023. As North I dealt and passed, East opened 1S, Blanch overcalled 2D, I raised to 3D, Blanch bid 3H, and I bid 3N. When dummy comes down, it is apparent that the opponents can cash at least 5 Clubs and the SA. On the lead of the S8 I have eight top tricks, but where is the ninth? The Heart finesse seems unlikely. So I need East to lead a Heart or a Spade. I desperately lead the CQ from dummy. When the expert East wins with the CK, it is “obvious” that I have CAJ as well as the SK, that his partner has the HA, and that his best shot is to lead to his partner’s HA and get a Spade back through me. His Heart play gives me my ninth trick. He was astounded when he realized what had happened.
Made the following impossible 3NT playing with Mark Blanchard at the national Lebhar IMP Pairs in New Orleans March 12, 2023. As North I dealt and passed, East opened 1S, Blanch overcalled 2D, I raised to 3D, Blanch bid 3H, and I bid 3N. When dummy comes down, it is apparent that the opponents can cash at least 5 Clubs and the SA. On the lead of the S8 I have eight top tricks, but where is the ninth? The Heart finesse seems unlikely. So I need East to lead a Heart or a Spade. I desperately lead the CQ from dummy. When the expert East wins with the CK, it is “obvious” that I have CAJ as well as the SK, that his partner has the HA, and that his best shot is to lead to his partner’s HA and get a Spade back through me. His Heart play gives me my ninth trick. He was astounded when he realized what had happened.
I loved the New Orleans Nationals, with one sorry exception: the literary quality of the limericks. To remedy this unfortunate situation, I hereby submit the following (featured on the May 4, 2023, Sorry Partner podcast):
While trying my hand at Pairs Silly*
I suddenly brought out Gazilli.
Pard jumped to a grand
With no Ace in his hand;
I guess I’ll just have to Ask Billy.
*term for the Silidor Pairs, courtesy Adam Grossack.
 See also TV clip (opening with the back of my head) from Good Morning New Orleans.
See also TV clip (opening with the back of my head) from Good Morning New Orleans.
5th January 2023, 07:42 am
January
Friends with Money (Netflix)
Troy (Paris killed Achilles killed Hector killed Menalaus, Breseis killed Agamemnon killed Priam; Netflix)
We Were Soldiers (Mel Gibson, Vietnam, Netflix)
The God Committee (pig heart, Kelsey Grammar, Netflix)
The Sound of Music: From Fact to Phenomenon (1994) – Julie Andrews, Christopher Plummer, Robert Wise (YouTube)
Continue reading ‘Books and Movies 2022’ »
Category:
Articles |
Comments Off on Books and Movies 2022
28th November 2022, 10:24 pm
 I had this progressive squeeze at Phoenix Nationals playing with Farley Mawyer in the 10K IMP Pairs. I was E playing in NT. South led the S10. I won the Q, unblocked the K, and led the HQ. North took the Ace and played Diamonds. I won the third one and cashed two Hearts and two Spades. On the last Spade, North holding — 10 Q K5 was squeezed and discarded the DQ. Now on the D9 he was squeezed again, and graciously threw in his cards.
I had this progressive squeeze at Phoenix Nationals playing with Farley Mawyer in the 10K IMP Pairs. I was E playing in NT. South led the S10. I won the Q, unblocked the K, and led the HQ. North took the Ace and played Diamonds. I won the third one and cashed two Hearts and two Spades. On the last Spade, North holding — 10 Q K5 was squeezed and discarded the DQ. Now on the D9 he was squeezed again, and graciously threw in his cards.
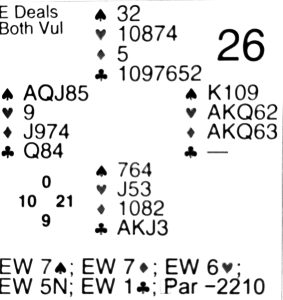 The second day I picked up KT9 AKQ62 AKQ63 —. I opened 2C, planning an auction such as 2C 2D 2H (Kokish) 2S (forced) 3D …, ending in 6H or 6D. But my partner’s response to 2C was a surprise 2S. So I just bid 7S. When the lead of D5 wasn’t ruffed, partner could claim.
The second day I picked up KT9 AKQ62 AKQ63 —. I opened 2C, planning an auction such as 2C 2D 2H (Kokish) 2S (forced) 3D …, ending in 6H or 6D. But my partner’s response to 2C was a surprise 2S. So I just bid 7S. When the lead of D5 wasn’t ruffed, partner could claim.
Category:
Articles |
Comments Off on Progressive Squeeze in Phoenix
20th November 2022, 08:32 pm
Dedication of the Frank Morgan Library in the Department of Mathematics and Statistics at Williams College, November 19, 2022.
Cutting the ribbon (video). 







My remarks (click for video): Thank you. Mihai asked about this tiling discovered by students here. I had a paper with 8 students on the best unit-area pentagonal tile, where best means shortest perimeter. Of course the best triangular tile is the equilateral triangle, the best quadrilateral tile is the square, and for six or more sides, the regular hexagon is best of all. Unfortunately the regular pentagon does not tile. The best pentagon is a tie, between the prismatic tile here which looks like a house, and the Cairo pentagon which I’ve seen on the streets of Cairo. Successive students discovered that you could mix the two types as in this beautiful tiling you see here and in Colin Adams’s new book on tilings.
Now some deeper history. When I first came to Williams I found in the old Bronfman a wonderful, distinctive math-stats library, with faculty offices around the perimeter opening onto the library. Those who went before, such as Guil Spencer, who served as chair for 18 years, had paid careful attention to every detail of the plans. For our students it was a favorite place to study, and we’d continually meet and greet them and each other there, sharing mathematics and statistics and often pulling a book from the shelves.
When the old Bronfman was knocked down it seemed that this space would be lost. But thanks to the persistent efforts of faculty, staff, and students, including the remarkable Students of Mathematics and Statistics Advisory Board, SMASAB, this library space as well as prominent classroom space has been preserved and enhanced. What a joy it is to look out today and behold all of that and more, to see all of you who have contributed to that spirit (I see the Horns of Horn Hall) and who have contributed to this place, and who are continuing that communal mission we all love and share. To me it’s the very essence of Williams: the community of faculty, students, and staff working together as colleagues to advance understanding. May Williams never lose that identity, through community such as you and spaces such as this.
Many thanks to Paul Collins, Joey Horn, Margaret, and Ellen Kennedy for photos and videos.
27th September 2022, 04:08 pm
In a drawing for the monthly NewTricks bridge tournament September 27, 2022, I won the chance to partner with Zia. Basically he just consistently plays good bridge. He generously emailed me three times about our convention card. We came in 3/20 with 63%, despite 5.6% for 6H-1 on a finesse and 22% when the opponents made 3N by a smart deep finesse in Hearts (Board 17 below). Zia made some of his characteristic deceptive plays, such as leading 2 from A962 in dummy’s Heart suit against 3D, leading 6 from QJ63 in dummy’s suit against 3N, and playing K from KQJ752 on my lead against 4C to make Declarer think his points were elsewhere. In my favorite example, Zia was playing 6C on Board 16 below. How to play the Spades? After drawing trump he immediately discarded the SJ on the HA and called for a low Spade from the Board. Of course his RHO, now imagining Zia with the stiff K and not wanting to hesitate (and realize if Zia started with doubleton KJ he would thrown both on the Hearts), would pop up with the A if he had it, saving Zia from the guess. Otherwise Zia could let the 9 ride. Of course on this particular layout, he couldn’t go wrong.
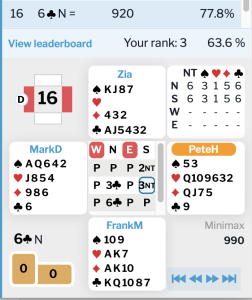
You can watch our whole match with expert commentary at
https://www.youtube.com/watch?v=XTJ_hN4IZxk
And my NewTricks “Challenge an Expert” Peter Crouch
And my NewTricks “Pros vs. Patrons” Part 1 Part 2
Continue reading ‘My Game with Zia’ »
Category:
Articles |
Comments Off on My Game with Zia
17th June 2022, 05:52 am

 Had a lucky 6H on Thursday June 17, 2022, at the festive Father’s Day game at the Cape May County Duplicate Bridge Club of the amazing Karen Sylvester. As North I opened 1H. My partner responded with a game-forcing 2C instead of showing 4-card support by Jacoby 2N or more accurately 3H with this 12-count. We soon arrived at a unpromising 6H. The DK lead gave a glimmer of hope if East also held the SK and I could locate the CQ, now probably with West. After drawing trump and clearing Clubs, I put East in with a Diamond. Afraid of giving up a ruff-discard by leading Clubs or Diamonds, East returned a Spade, giving me the SQ and the slam.
Had a lucky 6H on Thursday June 17, 2022, at the festive Father’s Day game at the Cape May County Duplicate Bridge Club of the amazing Karen Sylvester. As North I opened 1H. My partner responded with a game-forcing 2C instead of showing 4-card support by Jacoby 2N or more accurately 3H with this 12-count. We soon arrived at a unpromising 6H. The DK lead gave a glimmer of hope if East also held the SK and I could locate the CQ, now probably with West. After drawing trump and clearing Clubs, I put East in with a Diamond. Afraid of giving up a ruff-discard by leading Clubs or Diamonds, East returned a Spade, giving me the SQ and the slam.
Category:
Articles |
Comments Off on Lucky 6H at Cape May
15th April 2022, 01:10 pm
In a talk at Columbia University today (April 15, 2022), Gary Lawlor announced and described his proof that the standard triple soap bubble in R^3 is the least-perimeter way to enclose and separate three equal volumes.
Update 5/19/22: Milman and Neeman post proof of general triple and quadruple bubble conjectures in R^n and S^n https://arxiv.org/abs/2205.09102. See my review at https://amathr.org/milman-and-neeman and the beautiful Quanta article by Erica Klarreich.
Update 7/18/23: Milman and Neeman post proof of quintuple bubble conjecture as promised https://arxiv.org/abs/2307.08164.

6th April 2022, 04:50 am
Regularity theorems for compound bubbles or immiscible fluids require that the weights satisfy triangle inequalities. For example, if the interface between two regions of prescribed planar areas has high cost, two tangent disks minimizes weighted perimeter.
Here we note that even existence requires triangle inequalities, even for three fluids. Consider weight 3 for the 01, 02, and 12 interfaces (and weight 1 fo the rest), with say unit areas for 1 and 2 and small area for 3. Now the minimizer should be some kind of 12 double bubble inside a 3 bubble, with 13 and 23 interfaces coinciding with 30 interfaces. At a singularity, 13 and 30 interfaces meeting tangentially and then coincide, conjecturally the only new type of singularity.
Inspired by a question from Gary Lawlor.
Category:
Articles |
Comments Off on Even existence requires triangle inequalities
10th December 2021, 08:10 pm
Much enjoyed the festive Christmas party bridge games at Karen Sylvester’s Cape May County Duplicate Bridge Club December 9 and Martin de Bruin’s Shore Bridge Club December 10 (thanks to Terri U’Prichard). Great refreshments included Jane Havighurst’s cinnamon cake. Roger Read and I had a fortunate 76% game.
Category:
Articles |
Comments Off on Christmas Bridge at the Shore
29th November 2021, 08:24 am
After partners had to cancel, I paid to play in Nail Pairs with Michael Berkowitz, son of David and Lisa Berkowitz, a clear and friendly teacher, a member of the board of the Educational Foundation. With a 63.86% game in the second session, we qualified for the finals and earned 7. 27 Platinum points. One highlight was this squeeze at 3N for an overtrick for a tie for top. (See below; actual bidding was 1N 3N. Double dummy makes just 3N.) East led the H6 and then overtook his partner’s Q to return a third Heart to my Ace. After three rounds of Clubs ending in my hand, I advanced the S10, East failing to cover, to isolate the Spade menace to East who was also guarding the Hearts. In the end position I was on the board with SA7 and D2, with HA5 and DA in my hand. East could not guard both suits and had actually chosen to unguard the Hearts, so I played the Aces of Spades and Hearts and won the last trick with the H5 in my hand.

Continue reading ‘With Michael Berkowitz at Fall 2021 Austin Bridge Nationals’ »
Category:
Articles |
Comments Off on With Michael Berkowitz at Fall 2021 Austin Bridge Nationals
 Made the following impossible 3NT playing with Mark Blanchard at the national Lebhar IMP Pairs in New Orleans March 12, 2023. As North I dealt and passed, East opened 1S, Blanch overcalled 2D, I raised to 3D, Blanch bid 3H, and I bid 3N. When dummy comes down, it is apparent that the opponents can cash at least 5 Clubs and the SA. On the lead of the S8 I have eight top tricks, but where is the ninth? The Heart finesse seems unlikely. So I need East to lead a Heart or a Spade. I desperately lead the CQ from dummy. When the expert East wins with the CK, it is “obvious” that I have CAJ as well as the SK, that his partner has the HA, and that his best shot is to lead to his partner’s HA and get a Spade back through me. His Heart play gives me my ninth trick. He was astounded when he realized what had happened.
Made the following impossible 3NT playing with Mark Blanchard at the national Lebhar IMP Pairs in New Orleans March 12, 2023. As North I dealt and passed, East opened 1S, Blanch overcalled 2D, I raised to 3D, Blanch bid 3H, and I bid 3N. When dummy comes down, it is apparent that the opponents can cash at least 5 Clubs and the SA. On the lead of the S8 I have eight top tricks, but where is the ninth? The Heart finesse seems unlikely. So I need East to lead a Heart or a Spade. I desperately lead the CQ from dummy. When the expert East wins with the CK, it is “obvious” that I have CAJ as well as the SK, that his partner has the HA, and that his best shot is to lead to his partner’s HA and get a Spade back through me. His Heart play gives me my ninth trick. He was astounded when he realized what had happened. See also TV clip (opening with the back of my head) from Good Morning New Orleans.
See also TV clip (opening with the back of my head) from Good Morning New Orleans.














 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the