Frank Morgan

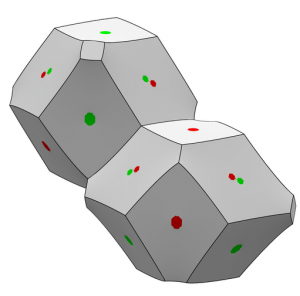Karoly Bezdek has proved that a partition of space into convex polyhedra of bounded diameters containing unit balls has average surface area at least 24/√3 ~ 13.86 and conjectures that the minimum is 12√2 ~ 16.97, given by rhombic dodecahedra. Ken Brakke has computed that if one allows arbitrary cells containing unit balls, the rhombic dodecahedra still beat the Kelvin (~17.83) and Weaire-Phelan (~21.15) foams, but they can morph into a “draped Williams cell” (thumbnail at right from nice picture at Brakke) with average area about 16.957, conjectured to be optimal.

Select episodes of my live call-in MathChat TV show are now available on YouTube:

February 11, 1996 with co-host Eric Watson ’97

March 2, 1996 with co-host Aaron Dupuis ’99

April 13, 1997 with special guest Benoit Mandelbrot

October 6, 1997 with special guest John Conway, at Princeton University

November 24, 1997 with special guest Freeman Dyson, at Princeton University

The first three are at Williams on Willinet.

Also check out my MathChat column archive and my Math Chat book. Continue reading ‘MathChat Videos’ »

ICMS workshop on “Isoperimetric problems, space filling, and soap bubble geometry” in Edinburgh, Scotland, March 19-22, 2012, described in my Huffington Post blog on “Soap Bubbles in Scotland”; research blog.

Video of Simon Cox, Aberystwyth University, organizer. Continue reading ‘ICMS “Isoperimetric Problems…” 19-22 March 2012 Edinburgh’ »

On the occasion of its centennial, the Royal Spanish Math Society has published a commemorative issue of their Revista. Mathematicians describe some early influential encounters with mathematics.

Continue reading ‘Mathematicians Tell Stories’ »

Yes, Thomas Hales proved that regular hexagons provide the least-perimeter way to tile the plane with unit-area tiles, even allowing them all to have different shapes:

Continue reading ‘Pentagons Everywhere’ »

After Hales proved in 1999 the Hexagonal Honeycomb Conjecture—that regular hexagons provide the least-perimeter, minimal-interface way to tile the plane with unit areas—I decided I wanted hexagonal tiles for my kitchen:

In the middle of the job, the contractor ran out of grout for the interfaces between the tiles. He had an excuse: he explained that hexagonal tiles apparently required more grout! That was the wrong time and place for that excuse. I had to respond: “Actually…”.

Guest post by Professor Deb Bergstrand, Swarthmore College

Ed Burger’s invited MathFest address on recent work in number theory was masterful.  He wowed the crowd at the end when he revealed that the new results he presented were discovered by his SMALL undergraduate research students during the summer of 2010, thus reinforcing his message that the mathematics of tomorrow will be produced by the students of today. Ed’s other direct role at the conference was the invited paper session he organized on “Offering students lessons beyond mathematics, through mathematics.” Continue reading ‘Good Times at MathFest 2011 in Lexington’ »

When I visited Universiti Teknologi Mara in Kuala Lumpur, Malaysia, I was most impressed by the young mathematician who presided at my session, Nuru’l-‘izzah Othman. She summarized the session as follows, better than I could have:

Three golden rules for starting a mathematics project:

1.  Start small. Try to start with small and manageable projects and avoid being too ambitious.

2.  Start with something familiar or close to one’s heart.

3.  Do what you enjoy doing and enjoy what you are doing. Continue reading ‘World Peace through Mathematics’ »

At the Math, Science, Technology Conference at Exeter in June, I met high school mathematics teacher Patricia Heather-Lea. She shared with me and now with you a message she once drafted but never sent to her students:

“Dear students, I know that you can reach anyone, anytime, anywhere, using technology. I want you to know that you must not lose sight of the here and now, to be able to look into someone’s eyes, and say:

I am sorry;

I love you;

Forgive me.

This ability is critical to the present and the future of the human race.

Love, Mrs. Heather-Lea”

Jianguo Cao, who passed on in June, was a good mathematician and correspondent. It was his paper with Itai Benjamini on the isoperimetric problem in surfaces of revolution that first proved, for example, that isoperimetric curves in the paraboloid {z=x²+y²} are horizontal circles. Many papers followed by many mathematicians, including me.

After writing a joint paper with Hugh Howards and Michael Hutchings and returning from leave, in cleaning out old files I discovered a preprint of Cao’s paper with Benjamini which Cao gave me at the Lehigh Geometry/Topology Conference in June, 1994. I forgot all about it and got interested in the problem two years later. The basic idea of our Theorem 2.1 came from Hutchings in an email message of December 19, 1996. But now I know that the first inspiration came from Cao.