Math, Teaching, and Other Items of Interest
Archive for the ‘Math’ Category.
In Barcelona, Robert McCann talked about his work with Jonathan Korman and Christian Seis on optimal transportation with a constraint h(x,y) on the flow from x to y. A constant constraint h means that an x must be spread out over at least fraction 1/h of the target; there is not the capacity to send it all to the most desirable spot. Here we present a simplified extension of some of their results. Continue reading ‘Optimal Transportation with Constraint’ »
Sixty mathematicians and students gathered in Barcelona at the Center for Research in Mathematics CRM for a Conference on Qualitative and Geometric Aspects of Elliptic PDEs, proficiently organized by Xavier Cabré, Daniele Castorina, Manel Sanchón, and Enrico Valdinoci.
In my talk I mentioned a new isoperimetric theorem by Xavier Cabré and his students Xavier Ros-Otón and Joaquim Serra, which they describe in this video. Continue reading ‘Geometry and PDEs in Barcelona’ »
The famous Wallet Paradox invites two similar individuals to lay their wallets on the table, the one with the lesser amount of money to win both. Paradoxically, each might reason: “I have the advantage, because if I lose, I lose just what I have, but if I win, I win more than I have.” A follow-up analysis assumes that each has the same expected amount of money and asks for the best probability distribution or “best strategy” with that given mean. The following note is based on a senior colloquium talk. Continue reading ‘Pradham ’13 on Wallet Paradox’ »
Note added 5 June 2016. A noncompact counterexample is given by Nardulli and Pansu, arxiv.org. On the positive side, see the comment below by Milman and Flores/Nardulli [FN].
Note added 21 March 2018. A 2D (noncompact) counterexample is given by Papasoglu and Swenson [PS], via expander graphs.
Given a smooth Riemannian manifold, the isoperimetric profile I(V) gives the infimum perimeter of smooth regions of volume V.
Proposition 1. In a compact smooth Riemannian manifold of dimension at least two, the isoperimetric profile is continuous. Continue reading ‘Isoperimetric Profile Continuous?’ »
Jian Ge’s recent ArXiv post on “Comparison theorems for manifolds with mean convex boundary,” Theorem 0.1, has a generalization to manifolds with density, here within a factor of 2 of sharp for constant density: Continue reading ‘Distance to Boundary of Manifold with Density’ »
In Rn or in a Riemannian manifold, one may consider regions R with density given by an integrable nonnegative function g, with volume ∫R g. If everything is smooth, the perimeter is given by ∫∂R g, or more generally by Stokes’ Theorem. For finite perimeter, these are the so-called normal currents of geometric measure theory. All of this can be done in a manifold with density f (unrelated to g).
In Rn, if you allow regions with density, there is no isoperimetric optimum for given volume, because large balls with low (constant) densities approach perimeter 0; similarly in any space for which P/V has no minimum. In a space of finite volume, such as Gauss space Gn (Rn with Gaussian density) there is an optimum: the whole space with appropriate constant density has perimeter 0. At the other extreme, in R with density exp(x3), a left halfline with high density approaches perimeter 0.
Note that if a region with density is isoperimetric, it remains so for all multiples of that density.
In principle one may allow regions with variable density f, the variability contributing to the boundary, but since any such region is an integral of regions Rd = {f ≥ d} with constant density d, one need consider only regions with constant density.
For a manifold with density with isoperimetric profile P = I(V), the least-perimeter region with density with unit volume just minimizes cI(1/c); in a space of infinite volume its perimeter to volume ratio is the Cheeger constant inf P/V.
In R2 with density exp(r2), where classical isoperimetric regions are balls about the origin, among regions with density the isoperimetric optimum for every area is the same disc of radius r ~ 1.1 (solution to exp(r2) = 2r2 + 1) with appropriate constant density.
Proposition. In Rn with smooth, uniformly log-convex radial density f(r), an isoperimetric region with density exists.
An ingredient in proving the existence of isoperimetric regions and clusters of prescribed volume(s) is the boundedness of isoperimetric regions of smaller volume(s). One proof of boundedness is by monotonicity. The proof in my Geometric Measure Theory book (Lemma 13.6) uses a non-sharp isoperimetric inequality for small volume and has the advantage of applying to convex integrands more general than area; the requisite isoperimetric inequality follows immediately from the isoperimetric inequality for area. All of this works equally well in the presence of a density. For more delicate results see
Frank Morgan and Aldo Pratelli, Existence of isoperimetric regions in Rn with density, Ann. Global Anal. Geom. (2012); arXiv.org (2011)
and Cinti and Pratelli.
My book comments that existence similarly holds in any smooth Riemannian manifold M with compact quotient M/G by a group of isometries. Monotonicity still yields boundedness; even with density (bounded above and below by compactness) the classical mean curvature is bounded and hence classical monotonicity applies. To use my alternate proof, which applies to more general integrands, one needs the isoperimetric inequality for small volume, which follows immediately from such an isoperimetric inequality for area without density. For the latter in a more general setting, see Theorem 2.1 of Morgan and Ritoré “Isoperimetric regions in cones” after Berard and Meyer. In this simpler setting of M/G compact, you can just cover M with congruent balls with a bounded number of balls meeting each point and apply the relative isoperimetric inequality in each ball. Incidentally the same covering can be used to replace the division into cubes in the existence proof 13.7 in my book.
“Analysis and Geometry in Metric Spaces” is one of a number of new open access journals to be funded by author fees, such as the Gowers-Tao Forum of Mathematics. The idea is that long-term it will be much cheaper for institutions to pay author fees than subscription fees, but the transition will be difficult, since while the major journals are on the old model, institutions cannot drop their subscriptions and may not pay author fees, and authors would rather publish for free in established journals.
“Analysis and Geometry in Metric Spaces” provides a journal for an important and rapidly growing modern area of mathematics and to its credit it does it on this new open access model of the future. I wish my good friend and the editor Manuel Ritoré of the extraordinary Department of Geometry and Topology at the University of Granada every success.
Steve Zottoli and I, in attempting to model biological cells, came up with the following theorem on the shape of planar double cells in which the tension of an interface is a strictly convex function of the linear density. One could conjecture a similar result in 3D.
Theorem. For a double planar cell of prescribed areas A1, A2, consisting of three interfaces of prescribed mass meeting at two points, the configuration of least energy, computed for each interface as the integral of the tension with respect to arclength, is given by three circular arcs of constant density, as in Figure 1. The angles at which they meet are determined by tension equilibrium and their curvatures ki and tensions ti satisfy
k1t1 = k2t2 + k3t3.
This is the same as the energy minimizing cluster for two immiscible fluids inside a third.
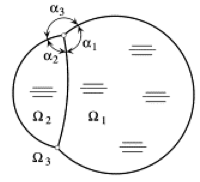
Figure 1. An energy-minimizing double cell consists of three circular arcs in equilibrium. Figure from Slobozhanin and Alexander.
Remark. Even if the enclosed masses instead of areas are prescribed, the minimizer will still be minimizing for whatever areas it has and will hence have the stated form. If total mass rather than the mass of each interface is prescribed, then each interface will have the same density and tension and the double cell will be the same as the energy minimizing soap bubble cluster, with angles of 120 degrees.
Proof. A minimizer has constant density on each interface (because on any fixed curve of prescribed mass, constant density uniquely minimizes energy, because tension is a strictly convex function of density). Circular arcs are best. A fortiori, the minimizer minimizes weighted length, with a different weighting constant for each interface, which is the immiscible fluids problem.
Remark. The immiscible fluids problem can be posed in great generality in geometric measure theory [M1, Chapter 16], allowing very general, disconnected regions. That the minimizer still takes the above form can be proved by the same simple argument that Hutchings [M2] provided for the case when all weightings are equal, the “double soap bubble problem,” as was pointed out by Cotton and Freeman [CF, §2.1].
[CF] Andrew Cotton and David Freeman, The double bubble problem in spherical and hyperbolic space, Intern. J. Math. Math. Sci. 32 (2002) 641-699.
[M1] Frank Morgan, Geometric Measure Theory: a Beginner’s Guide, Academic Press, third edition, 2000.
[M2] Frank Morgan, Proof of the double bubble conjecture, Amer. Math. Monthly 108 (March 2001) 193-205.
The Weaire-Phelan soap bubble foam counterexample to Kelvin’s Conjecture is the latest art exhibit on the roof of the Metropolitan Museum of Art in New York City (photo from New York Times article). It is conjectured to divide space into unit-volume chambers with the least amount of material. It was also used for the Beijing Olympic Water Cube. For more on the Kelvin Conjecture, see my blog at the Huffington Post.
Note added 8 July 2012. Rob Kusner pointed out this canopy, designed by Giancarlo Mazzanti, in Bogotá, Columbia, reported by Michael Kimmelman in The New York Times.
Welcome to my blog. I also have a blog at the