New Optimal Pentagonal Tilings
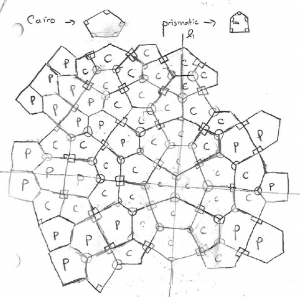
Updated with new discoveries 31 January —11 February 2015 and 3 April 2019; first published 27 May 2014. (Incidentally, new type of pentagonal tile discovered July 2015 by Casey Mann, Jennifer McLoud-Mann, and David Von Derauc. And that’s it, as proved July 2017 by Michaël Rao, arX). For these examples and a proof that symmetry groups with order three rotations cannot occur, see John Berry, Matthew Dannenberg, Jason Liang, Yingyi Zeng, Symmetries of Cairo-Prismatic tilings, Rose-Hulman Und. Math. J. 17 (2016), http://scholar.rose-hulman.edu/rhumj/vol17/iss2/3.
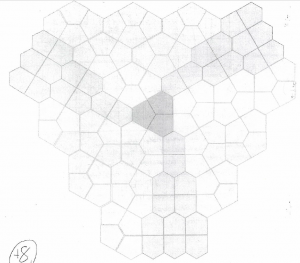
A joint paper [C1] with my SMALL undergraduate research Geometry Group found least-perimeter pentagonal unit-area tiles, Cairo and Prismatic:
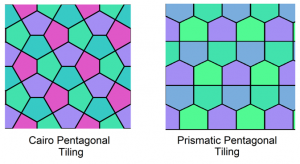They proved that mixtures of unit-area convex pentagonal tiles can do no better, but found many examples of Cairo-Prismatic tilings that do equally well [C1, C2], one appearing in the new Math Library at Williams:
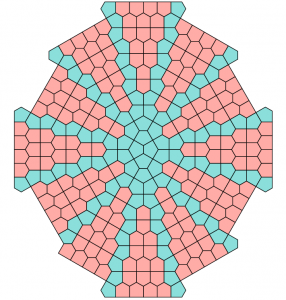
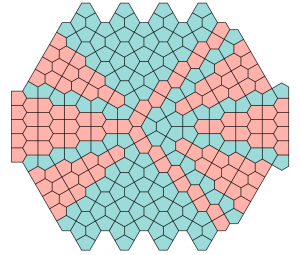
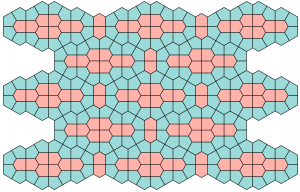
Since their work nine more have been discovered. The first four were found and rendered by one of the original coauthors, Maggie Miller. The first, “Double Pillbox,” adds p4 to p1, p2, p4g, and cmm as the fifth of the seventeen Wallpaper symmetry groups; will anyone find examples of the other twelve? We’d be happy to post any new examples here.
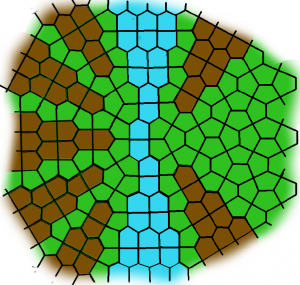
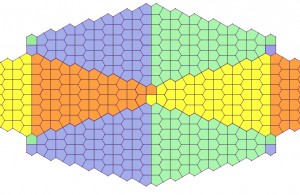
Double Pillbox River
Teeth Yellow Brick Road
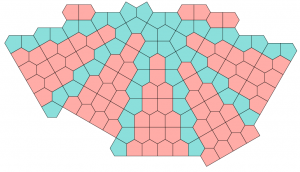
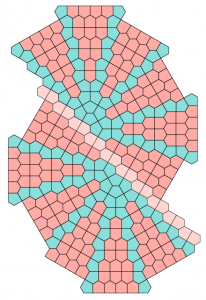
The next three came from students in Colin Adams’s Tiling class. Samantha Petti built one from a cardboard kit printed by Ben Hoyle (see various completions by Whitney below):
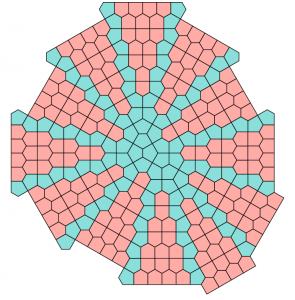
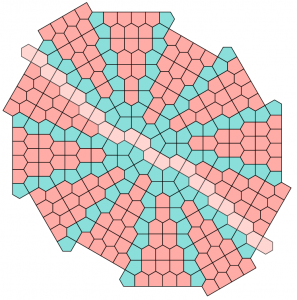
The last two were found by Victor Luo and by Lilliana Morris and Byron Perpetua:
Here are a nice rendering and variation on Luo by Glen Whitney, President of the national Museum of Mathematics (MoMath):
On Saturday January 24, 2015, MoMath premiered a working set of Cairo and Prismatic tiles and visitors discovered two new Cairo-Prismatic tilings:
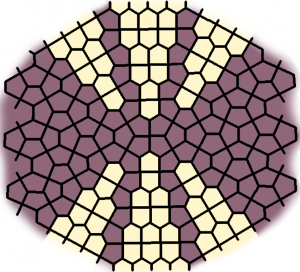
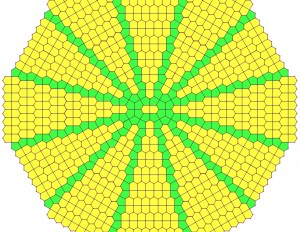
“Center Ice” by Christian Green
The first is by Silvano Bernabel and Daniel Tilkin. Bernabel writes:
“I’m a graduate student at Hunter college, where I’m studying pure math. I’m interested primarily in number theory. I really can’t imagine a world without mathematics. Math is the language of our reality, our universe, and with it we ask the strangest questions, because we can! It’s about observing without any rules and the only thing you’ll need is a little creativity. With MoMath you’re free to explore, to start over, and to have fun. Not only do you get to learn how math is connected to so many things, but you get to see how much people enjoy math, which is something you can’t see everyday.”
Tilkin writes:
“I’ve been interested in math since a young age. My father showed me how to solve problems and explore, and I’ve never really stopped. I majored in math and computer science at Carnegie Mellon. I currently work for G2 FinTech programming software for computing capital gains taxes. [Mathematics] teaches analysis skills which are increasingly important in today’s connected world. I’m proud to support MoMath in this mission. I hope to drop by MoMath soon and find some more, seems like there’s still a bunch out there waiting to be discovered.”
The second is by Christian Green, “I’d like to name it Center Ice because I play hockey.” He’s the goalie. His dad Dmitry writes:
“Christian is 10 yrs old in 5th grade at the Geneva School of Manhattan. He’s always been good at math and particularly determined with tessellation problems. Those are his favorite ‘because they go on forever.’ We’ve been going to MoMath since it was still a traveling exhibit; we first went there two or three years ago in a gymnasium on the Upper East Side, and were very excited to hear about a permanent home. Christian has been enjoying it all these years because ‘you can play with math there.’ Thank you for hosting the wonderful event, and tolerating us after hours while Christian finished his tiling. He just couldn’t drop it.”
Brian Chung verified their novelty and remarked:
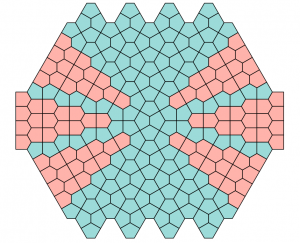
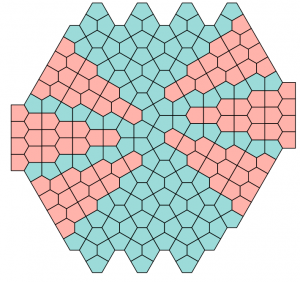
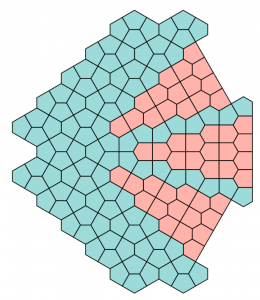
“The first one can be viewed as a variant of the Christmas Tree [C1, Fig. 11], where they keep only two of the trees and keep expanding, and the filling on the two sides are replaced by four towers and blocks of the four-Cairo hexagons. The second one is the Plaza [C1, Fig. 13], with a row of Prismatics squeezed into the middle.”
Christmas Tree and Plaza [C1, Figs. 11, 13]
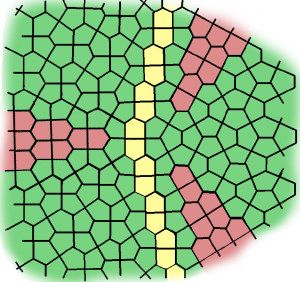
Glen Whitney, President of MoMath, enhanced Petti’s image above
and discovered that it can be completed in many ways: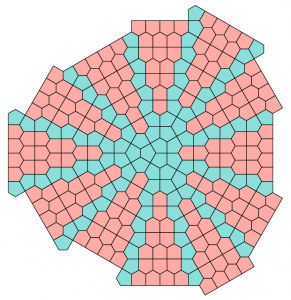
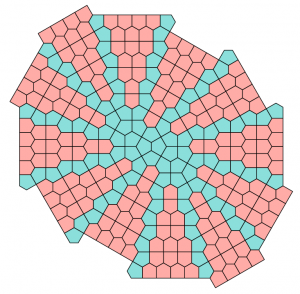
Whitney writes: “Petti2 through Petti5 have various rivers through them, into which a strand or multiple parallel strands of prismatics can be inserted, as in Petti3r and Petti5r below. Petti3r illustrates that rivers can meander and Petti5r illustrates that when the river happens to be straight you get a two-parameter infinite family of tilings, parametrized by the width of the river (you can also of course use Cairo-assembled hexagons for the river in this straight case) and by how far one half is displaced along the river from the other. There are other distinct rivers in Petti3 and Petti5 as well, and rivers in Petti2 and Petti4.
P.S. 6Feb’15 from Whitney: “I just realized that Petti2 is none other than the Marjorie Rice Cairo-Prismatic tiling listed in the Notices paper [C1, Fig. 6].”
11Feb’15. Whitney reports three new discoveries at a MoMath staff session:
“Three Towers” by Alex Gelman, “Toothy Smile” by Ester Schewel and Gemma Gearhart, and “Space Pills” by David Anderson and Heather Gordon. The second is like Teeth but with an extra 120-degree bent path in it. The third is haflway between Spaceships and Pills. Present and contributing also Sook Ramsaroop, Shaterra Overton, Susan Rubin, Ana Hocevar, Jeff Branzburg.
3April’19. Dave Smith has more examples on his webpage hedraweb.wordpress.com.
Send new examples to me for posting here.
[C1] Ping Ngai Chung, Miguel A. Fernandez, Yifei Li, Michael Mara, Frank Morgan, Isamar Rosa Plata, Niralee Shah, Luis Sordo Vieira, Elena Wikner, Isoperimetric pentagonal tilings, Notices AMS, 2012.
[C2] Ping Ngai Chung, Miguel A. Fernandez, Niralee Shah, Luis Sordo Vieira, Elena Wikner, Perimeter-minimizing pentagonal tilings, Involve 7 (2014), 453-478
I just enjoyed the YouTube video of your recent Celebration of Mind presentation on optimal pentagon tilings. Now I’m very sorry I had to miss the live presentation!
I’m guessing you already know this, but I thought I’d share it just in case. All of the mixed Cairo-prismatic pentagon tilings can be constructed with vertices in a vector space over Z[√3], the ring extension of the integers with √3. In more straightforward terms, every X or Y coordinate value can be expressed as A+B√3, for integers A and B.
As a demonstration, here is a model I built in vZome, my geometry application, drawn using vectors in that space:
https://vzome.com/app/embed.py?url=https://raw.githubusercontent.com/vorth/vzome-sharing/main/2021/08/27/19-39-03-cairo-prismatic-pentagon-tiling/cairo-prismatic-pentagon-tiling.vZome
(You may notice some rendering oddities, with the vertices and edges flickering in and out, or even the whole design getting clipped off. Those are just defects in my web viewer, sorry!)
The model is the “Spaceship” tiling from your video. When you mentioned that all the angles were 120 degrees and 90 degrees, I recognized that those angles could be supported in the √3 ring. The only remaining question was the lengths, but that actually answered itself, since one pentagon is constructed with four equal-length edges, so if those edges are constructible, then the 5th edge is also constructible.
vZome might make a nice tool for people exploring these tilings, since you are drawing in such a constrained way. It is not as good as just dragging out pentagon tiles that snap to vertices, but it is a lot better than freehand with Illustrator!
vZome is a free application, so I’m not selling anything. There is a desktop app for Mac, Windows, and Linux, and that is where you can create designs. It was originally built to support Zometool, another constrained vector space, but I’ve extended it to other fields (or rings). Last year I built the web viewer, and a mechanism to share models through Github with very little friction.
Best regards,
Scott Vorthmann
G4G Board Member
https://vzome.com
Welcome to my blog. I also have a blog at the
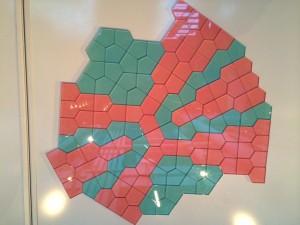
David Smith:
I like these. Pity that the prismatic tiles only fit together one way (base to base).
23 October 2018, 11:58 am