Frank Morgan

Just as a a soap bubble minimizes surface area, crystals minimize a more general energy depending on orientation with respect to the underlying crystal lattice, given by integrating some (continuous) norm on the unit normal. (One might drop the usual assumption that a norm is even.) The optimal shape is the unit ball of the dual norm, called the Wulff crystal (see [M2, Chapt. 16]).

Just as one considers soap bubble clusters, tending to minimize surface area for prescribed volumes, one considers crystal clusters, with the energy of an interface between the i^th and j^th crystals given by a norm F_ij. For the case of immiscible fluids, each F_ij is some constant a_ij on unit vectors, a multiple of the usual surface energy. For lowersemicontinuity and the existence of minimizers one needs triangle inequalities a_ik ≤ a_ij + a_jk, since otherwise an interface between the i^th and k^th crystals could profitably be replaced by a thin layer of the j^th crystal. For general norms, the lowersemicontinuity hypothesis is more subtle (see [M2]). Given lowersemicontinuity, existence follows after Almgren [A] as simplified, clarified, and generalized by Morgan (see [M2, Chapt. 16]). Almgren considered certain multiples of a single norm, but allowed the norm to depend on position as well as direction. In this context he proved regularity almost everywhere. For the more general problem, regularity is known only in the plane [MFG].

The optimal double soap bubble was proved by Foisy et al. [F] in R², by Hutchings et al. [HMRR] in R³, by Reichardt et al. [RHLS] in R⁴, and by Reichardt [R] in Rⁿ. Cotton and Freeman [CF, Thm. 2.4] noted that the simpler planar double soap bubble proof by Hutchings [M3, §3] applies to immiscible fluids. Lawlor [L] provided a beautifully simple proof in Rⁿ. He introduced a powerful new technique, which he called unification, which by simultaneously considering all pairs of volumes and all weightings produced much stronger equilibrium conditions. He also provided a striking new symmetry argument, remarkably independent of regularity, with wide potential application.

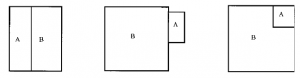
Less is known about optimal double crystals for more general norms. Zucker et al. [Z] compute some examples. For the case where all three norms are the l¹ norm in the plane, Morgan et al. [MFG] proved that the minimizer comes in three types, depending on the relative size of the smaller crystal:

Wecht et al. [WBT] proved similar results for three multiples of the l¹ norm.

In June 2014, at a conference in Pisa on “Isoperimetric Problems…”  (organized by Aldo Pratelli, Guido de Philippis, and Morgan), Jean Taylor, de Philippis, and Morgan talked over lunch about optimal double crystals. A familiar fact about planar soap bubble clusters is that if three curves emanate in equilibrium from a point (with constant curvatures summing to 0), then they all meet again (possibly at infinity in the case of three straight lines). This seems unlikely for a general norm, since all of the resulting equilibrium double crystals would have the same (minimum) energy. Instead, one might expect generically just four such equilibria, two yielding the two vertices of the unique minimum, and the other two yielding an unstable equilibrium in between (as promised by the mountain pass lemma). If the norm has four-fold symmetry, there would be two absolute minima and two unstable equilibria, etc. Maybe such behavior can happen without norm symmetry. For three given norms, it seems immediately implausible that they should always close up.

Consider an interpolation between the Euclidean and l¹ norms (with four-fold symmetry). For one prescribed area smaller than the other, there are apparently eight stable places to put it: four sides, four corners. If it is much smaller, the corners are the absolute minima; if it is only slightly smaller, the sides. I guess there are eight unstable equilibria in between. At one particular ratio, there are eight minima in two geometrically distinct families, and eight congruent unstable equilibria.

As pointed out by Taylor, more physically, one could allow three norms and rotations thereof.

References

[F] Joel Foisy, Manuel Alfaro, Jeffrey Brock, Nickelous Hodges, and Jason Zimba, The standard double soap bubble in R² uniquely minimizes perimeter, Pac. J. Math. 159 (1993), 47-59.

[HMRR] Michael Hutchings, Frank Morgan, Manuel Ritoré, Antonio Ros, Proof of the Double Bubble Conjecture, Ann. Math. 155 (2002), 459-489.

[M1] Frank Morgan, Lower-semicontinuity of energy of clusters, Proc. R. Soc. Edinburgh 127A (1997), 819-822.

[M2] Frank Morgan, Geometric Measure Theory: a Beginner’s Guide, Academic Press, 2009.

[M3] Frank Morgan, Proof of the double bubble conjecture, Amer. Math. Monthly 108 (3) (2001), 193-205.

[MFG] Frank Morgan, Christopher French and Scott Greenleaf, Wulff clusters in R², J. Geom. Anal. 8 (1998), 97-115.

[L] Gary Lawlor, Double bubbles for immiscible fluids in Rⁿ, J. Geom. Anal. 24 (2014), 190–204.

[R] Ben W. Reichardt, Proof of the double bubble conjecture in Rⁿ, J. Geom. Anal. 18 (2008), 172-191.

[RHLS] Ben W. Reichardt, Cory Heilmann, Yuan Y. Lai, and Anita Spielman, Proof of the double bubble conjecture in R⁴ and certain higher dimensional cases, Pac. J. Math. 208 (2003), 347-366.

[WBT] Brian Wecht, Megan Barber, and Jennifer Tice, Double salt crystals, Acta Crystallographica, Sect. A (Jan. 2000) 92-95.

[Z] Rachel V. Zucker, Dominique Chatain, Ulrich Dahmen, Serge Hage`ge, W. Craig Carter, New software tools for the calculation and display of isolated and attached interfacial-energy minimizing particle shapes, J. Mater. Sci. 47 (2012), 8290–8302.