Frank Morgan

Yes, Thomas Hales proved that regular hexagons provide the least-perimeter way to tile the plane with unit-area tiles, even allowing them all to have different shapes:

Some joint work with students (Ping Ngai Chung, Miguel A. Fernandez, Yifei Li, Michael Mara, Frank Morgan, Isamar Rosa Plata, Niralee Shah, Luis Sordo Vieira, Elena Wikner, Isoperimetric pentagonal tilings, Notices AMS, 2012) has found least-area tilings by convex pentagons:

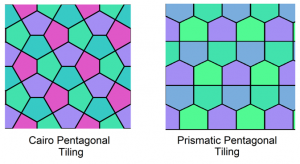
The Cairo tiles are popular in Cairo, as documented by David Bailey and Helen Donnelly, also here and references here. My colleague Steve Zottoli has observed that they appear in American concrete tiling by Daniel Ogassian

and that the second, Prismatic tile, often called a house, specifically looks like a corn crib:

(“Field guide to New England barns and farm buildings” by Thomas Durant Visser). Zottoli also found an article on an Iranian “800-year-old pentagonal tiling…” by Emil Makovicky in Fivefold Symmetry by Istvan Hargittai:

this dargah (shrine) of the mystic Hazrat Iniyat Khan via Roger von Oech:

examples from nature:

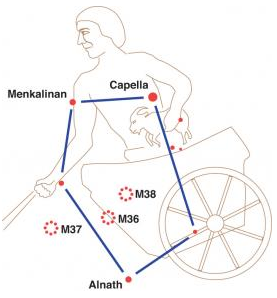
and from the heavens (via StarDate), Auriga the Charioteer:

Another colleague showed me pentagonal faces on pyrite (“Fools’ Gold”) and a model of the dodecahedral pyritohedron, which figured in the 1994 Weaire-Phelan counterexample to Kelvin’s Conjecture:

Pentagons are everywhere.

Note added 4 June 2012. There are 14 known types of convex pentagons that tile the plane. Three of the latter ones were discovered in the late 70s by amateur Marjorie Rice (homemaker, another noble profession), who had read about tilings in Martin Gardner’s column in her son’s issue of Scientific American. In 1985 Rolf Stein (U Dortmund) found the 14th. Bagina [B2, 2011] proves 8 edge-to-edge convex types (also Sugimoto 2012). Only in 1985 [HH] were the five types of tilings by a single equilateral convex pentagon proved complete (also [B1, 2004]); Hirschorn says they have unpublished classification for nonconvex equilateral.

[B1]   O. Bagina, Tiling the Plane with Congruent Equilateral Convex Pentagons, J. Combin. Theory. Ser. A , 2(105):221–232, 2004.

[B2]   O. Bagina, Tilings of the plane with convex pentagons (in Russian), Vestnik KemGU 4(48): 63-73, 2011.

[HH]  M. D. Hirschhorn and D. C. Hunt, Equilateral convex pentagons which tile the plane, J. Comb. Theory 39 (1985), 1-18.

Note added 30 October 2017. New type of pentagonal tile discovered July 2015 by Casey Mann, Jennifer McLoud-Mann, and David Von Derauc. And that’s it, as proved July 2017 by Michaël Rao, arX, In a rest area bathroom I found this pentagonal tiling:

Note 21 May 2018. “Tilings of Sphere by Congruent Pentagons IV” by Yohji Akama, Min Yan
There are exactly eight edge-to-edge tilings of the sphere by congruent equilateral pentagons. https://arxiv.org/abs/1805.07217