«
»

Rebalance Every (15000/V)^(1/3) Years

14th May 2010, 07:49 am
We give an oversimplified argument that an amateur investor with capital V should rebalance holdings every
(15000/V)^{1/3} years.
For example, with $15,000, rebalance annually. With $15 million, monthly. With $15 billion, every few days.
After we proved the advantage of (continuous) rebalancing in the log-optimal section of my Investment Math course, one of my students, Walter L. Filkins, asked me about how often to rebalance in practice, depending on capital V and perhaps transaction costs c, volatility, etc. The web seems to indicate that there is no received answer. We came up with an argument that suggests that you should rebalance every
(300c/2V)^{1/3} years,
which reduces to the above formula for c about $100. We decided not to use log-optimal analysis. The log-optimal portfolio assumes continuous rebalancing, which in practice cannot be approximated. The expected return between rebalancings is just the weighted average of the expected returns v_i of the various assets, so you miss the main log optimal rebalancing bonus \mu=v+\sigma^2/2.
Our model is much simpler. In some units of money or utility, optimal weighting gives you an expected return 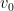v_0 (say on the order of .10), which without rebalancing falls off in time at an increasing rate, say
v=v_0-at^2.
Note that expected growth-rate at constant weights does fall off quadratically in the weights, but we’re using quadratic fall-off just as the most simple general model. Let’s say a is about .01, so that in a year v would fall from the optimal .10 to .09.
By rebalancing every s years, your average rate of return will be
(1/s)\int\limits_0^svdt=v_0-as^2/3.
Your transaction/time costs per year will be about c/s.
Your net profit per year will be
V(v_0-as^2/3)-c/s.
This is maximum when
s=(3c/2aV)^{1/3}.
For a = .01, this yields
s=(300c/2V)^{1/3}.
For c = 100, this becomes
s=(15000/V)^{1/3}.
Of course we could add a simple condition such as don’t rebalance if the transactions cost c is more than 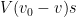V(v_0-v)s, roughly the expected benefit of rebalancing, i.e., for c say 100, don’t rebalance if
v_0-v<4V^{-2/3}.
Category: General interest, Math