Frank Morgan

Guest post by Jack Wadden ’11 from my Discrete Mathematics 251 class. For more on this topic google “paths in Pascal’s triangle,” e.g. Baez.

I was thinking today about Pascal’s triangle and how amazing it is that the binomial theorem actually works and why each number corresponds to a combination. It turns out that if you think of Pascal’s triangle as an upside down binary tree, this relationship is obvious. Continue reading ‘Pascal’s Triangle’ »

Guest post by Ville Satopaa ’11 from my Discrete Mathematics 251 class.

We all know of the famous Fibonacci sequence

0, 1, 1, 2, 3, 5, 8, 13, …

in which each term is the sum of the previous two.

When tends to infinity, the ratio between the 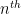term and the 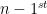term gets closer and closer to something that we call the Golden Ratio, denoted by :

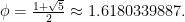
This ratio seems to define beauty to some extent. In fact, it turns out that a person with a beautiful face has nose, eye position, the length of chin and many other measurements of the face in the Golden Ratio. Here are some measurements that should follow the Golden Ratio:

1. length of the face / width of the face

2. width of the mouth / width of the nose

3. width of the eyebrows / the distance between the pupils.

4. outside distance between eyes / hairline to pupil

5. nose tip to chin / mouth to the chin

Well, are faces with ratios close to the Golden Ratio actually beautiful? Fortunately, it is easy to test this. Let’s pick a photo of an attractive person looking directly at the camera, so that it is easy to make the measurements.

Using this picture of Meghan Fox from exposay.com I measured the following ratios (the picture pasted to this file is of difference size):

1. 7.1 / 4.3 = 1.65116
2. 1.6 / 1.0 = 1.6
3. 3.3 / 1.9 = 1.73684
4. 2.9 / 2.1 = 1.38095
5. 2.0 / 1.3 = 1.53846
The mean ratio turns out to be , and the mean difference from the Golden Ratio turns out to be 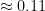. Therefore her face is overall quite close to the Golden Ratio. However, whether this provides evidence that the Golden Ratio can be used as an estimate of beauty depends on whether you consider Meghan Fox attractive or not. I personally do.

At Williams every senior math major chooses a faculty advisor and gives a 35/40-minute colloquium talk. Since we currently have over fifty senior majors, this keeps us pretty busy, but we think it well worth the effort.

Here is how I like my advisees to prepare, starting a month before the talk and consulting with me every day or two:

1. Outline of talk, with details of proofs.

2. Board drafts. Each page consists of exactly what is to be written on one section of blackboard. Each such board should convey one main idea, with a heading, a concise, abbreviated statement, and some kind of figure.

3. Draft rehearsal. Student sits down alone at keyboard and rehearses the talk by typing everything and then emailing it to me for comments and revisions.

4. Rehearsals at the blackboard, at least one with an audience recruited by the student.

5. Final rehearsal with me, ideally two days before the talk.

See also Lou Ludwig’s “Technically Speaking” video clips.

The Prime Number theorem says that the probability P(x) that a large integer x is prime is about 1/log x. At about age 16 Gauss apparently conjectured this estimate after studying tables of primes. Hugh Bray via Greg Martin suggested to me the following heuristic way to approach the same conjecture, which appeared in my Math Chat column on August 19, 1999:

Suppose that there is a nice probability function P(x) that a large integer x is prime. As x increases by the new potential divisor x is prime with probability P(x) and divides future numbers with probability 1/x. Hence P gets multiplied by  or roughly

The general solution to this differential equation is P(x) = 1/log cx.

Here’s a sketch of a movie idea about an excellent scientist and citizen, which I had had for some time, but which took further form during a cathedral mass in Granada in 1999. (There is also my “A Mathematician at Heaven’s Gate.”)

On the very day our scientist, Prof. Blake, retires he dies, and to his pleasant surprise finds himself at the Pearly Gates.

“It’s incredible, religion was right about this.”

“Are you concerned at all?”

“No, I’ve led a good life, and I’m sure this God must be good and appreciative.”

“What good have you done?”

“I’ve led the advancements in my field and been an upstanding member of the community.”

“What is good about such work?”

“Well, the purpose of humanity is to understand the universe, and I’ve contributed to that.”

“Do you think you did it because it was important, or because it appealed to you?”

“No, it is important.”

“Yes, though some folks find it easy to rationalize whatever they want to do. Why do you think you’ve been so successful.”

“Well, I’ve worked hard I guess, made myself organized and persistent and energetic.”

“And what do you think we should do with others who have been less successful, less organized and energetic?”

“Well, I guess you can’t just pretend it doesn’t matter. Maybe you could let them try again, with a fresh start.”

“Actually, we were wondering whether you might go back and finish up their work for them.” Continue reading ‘Scientist in Heaven’ »

A new ingredient in Hales’s 2001 proof of the Hexagonal Honeycomb Conjecture* is his Chordal Isoperimetric Inequality (see Chapter 15 of my Geometric Measure Theory book). It provides a lower bound on the perimeter of a bulging curvilinear polygon in terms of the extra area X enclosed by the bulges. With some help from my new colleague Steven Miller, I’ve realized that a minor modification of the proof improves the constant π/8 to the optimal π/4 as the requisite upper bound on X.

            To modify the proof, add to the auxiliary, less constrained problem the hypothesis that the longest chord is no longer than the sum of the lengths of the others. In the delicate case 1 < L₀ ≤ 2, by the hypothesis the length of the longest chord is at most L₀/2 and a minimizer consists of arcs of equal curvature over two chords of length L₁ = L₂ = L₀/2. If one of the arcs were more than a semicircle, X would exceed the area of a circle of unit diameter, π/4, a contradiction. Hence we are in the convex range of the arc function and the old convexity argument kicks in.

            Similarly if L₀ > 2, a minimizer conists of m ≥ 1 arcs over chords of length L_i = 1 and perhaps one lower arc over a chord of length 0 ≤ L_m+1 < 1. If any of the first m arcs were more than a semicircle, again the area under two would exceed π/4, a contradiction, putting us back in the convex range of the arc function and the old proof.

*The Hexagonal Honeycomb Conjecture says that congruent regular hexagons provide a least-perimeter way to partition the plane into unit areas.

When I spoke on Manifolds with Density (see Chapter 18 of the 2008 edition of my Geometric Measure Theory book)  at PIMS at the University of Calgary in September, 2008, Larry Bates asked for a generalization of parallel transport to an n-dimensional manifold M with density . For n=2, the generalized curvature  of a curve of Riemannian curvature involves the log of the density as well:

 =  

Since this describes the rate at which the unit tangent vector is turning, it can be used to define parallel transport.

            For n > 2, the generalized curvature vector  should be the Riemannian curvature vector minus the normal component of gradient of the log of the density. Along with the unit tangent,   determines a plane. Infinitesimally, vectors normal to the plane are transported by classical parallel transport. For vectors in plane, parallel transport is determined by generalized curvature. 

            Are there any applications?