15th March 2010, 08:06 am
Spaces M with metrics and measures, so-called metric measure spaces or mm spaces (see e.g. Gromov [G]), include very general singular manifolds and weighted graphs. In the smooth case, M is a Riemannian manifold endowed with a smooth positive function or “density” f; the prescribed measure is just f times the Riemannian volume. In freshman calculus one studies surfaces and solids of revolution via their generating curves and regions in the halfplane {x>0} with density f(x) = 2πx. All quotient manifolds of Riemannian manifolds and homogeneous spaces G/K are Riemannian manifolds with density, and mm spaces were previously called spaces of homogeneous type (see [CW, pp. 587, 591]). Another example, long important to probabilists, is Euclidean space with Gaussian density.
Continue reading ‘Manifolds with Density’ »
24th January 2010, 08:30 am
In reading prefaces to various works collected in the Harvard Classics (limited edition set no. 1312, purchased by my grandfather but never read, so that I had to slit open the folded pages with a knife), I was struck by the clarity and scope of the preface to Newton’s Principia. Newton announces an explanation of “the system of the World” by deducing the planetary orbits and the terrestrial tides by calculus from his new law of gravity. Then he says he wishes he could similarly derive “the rest of the phenomena of nature” from as yet undiscovered laws of attraction and repulsion between small particles. In the last sentence quoted below he explains how he deals with what was an annoying problem for writers before TeX. Continue reading ‘Newton’s Principia’ »
22nd November 2009, 09:06 am
In geometry the most fundamental inequalities are isoperimetric inequalities. In this post we will focus on dimension two, although all of the results extend to higher dimensions. In R2, the perimeter and area of a region satisfy
(1) P ≥ (4πA)1/2,
with equality for a round disc. On the unit sphere, for 0 < A < 4π,
(2) P ≥ (A(4π-A))1/2,
with equality for a geodesic disc.
In analysis, the most fundamental inequalities relate functions and often their derivatives. Continue reading ‘Functional Isoperimetric Inequalities’ »
29th October 2009, 05:46 am
Note added 13 June 2017: see a video featuring Prof. Johnson at the NESN Clubhouse.
In his senior colloquium last fall advised by Frank Morgan, Davide Carozza ’09 investigated the fastest path around the bases in baseball, assuming a bound of say 10 ft/sec2 on acceleration/deceleration. Following the baseline, stopping at each base, takes about 22.2 seconds. The standard recommended “banana” path follows the baseline maybe halfway to first base and then veers a bit to the right to come at first base from a better angle to continue towards second. That cannot be ideal. It would have been better to start at an angle to the right to head directly to an outer point on the banana path. Davide found that a circular path at 17.8 seconds is roughly 20% faster than following the baseline at 22.2 seconds. Stewart Johnson then computed the following optimal path at 16.7 seconds. The record time according to Guiness is 13.3 seconds, set by Evar Swanson in 1932 (with larger acceleration than our assumed 10 ft/sec2).
17th October 2009, 08:43 am
The celebrated Gauss-Bonnet formula has a nice generalization to surfaces with densities discovered by my 2004 undergraduate research Geometry Group. The classical Gauss-Bonnet formula relates the integral of the Gauss curvature G over a disc D to the integral over its boundary of the geodesic curvature 
:
.
One can weight arclength and area by densities:
.
Surfaces with density appear throughout mathematics, including probability theory and Perelman’s recent proof of the Poincaré Conjecture (see Chapter 18 of the 2009 edition of my Geometric Measure Theory book). Important examples include quotients of Riemannian manifolds by symmetries and Gauss space, defined as Rn with Gaussian density c exp(-r2).
The generalized Gauss curvature is given by
.
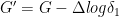Ivan Corwin and I have just written an article about this. The formula for how Gauss curvature changes under a conformal change of metric is a simple special case.
15th October 2009, 09:25 am
Write-up of a departmental faculty seminar, October 2, 2009.
Solutions to problems in geometry and physics and even in the social sciences tend to be symmetric. As prime example, the solution to the isoperimetric problem, which seeks the least-perimeter way to enclose given volume in R3, is a sphere, the most symmetric of all shapes. One way to prove this is to show that anything else improves as you make it more symmetric. For thousands of years, mathematicians have been looking for good ways to make shapes more symmetric and to prove that as they get more symmetric they “get better,” for example, enclose the same volume with less perimeter.
My favorite references are Burago and Zalgaller [BZ, §9.2] and Ros [R1, §3.2]. This talk is based on [MHH]. Gromov [G, §9.4] provides some sweeping remarks and generalizations, including most of our results.
1. Steiner symmetrization [St, 1838] replaces every vertical slice of a region in R3 with a centered interval of the same length, as in Figure 1. By calculus, the volume does not change, but one can show that the perimeter decreases (or remains the same).
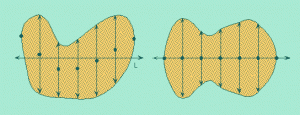
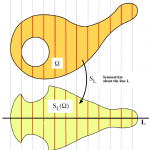
Figure 1. Steiner symmetrization replaces every vertical slice with a centered interval of the same length. www.math.utah.edu/~treiberg/Lect.html
Continue reading ‘Symmetrization’ »
11th June 2009, 01:25 am
My 2009 Williams College NSF “SMALL” undergraduate research Geometry Group has the following inequality for any 
function on the unit interval and for any p ≥ 1:
with equality for constant functions and if p>1 only for constant functions. They conjecture that these results still hold if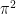 
on the right-hand side is replaced by 
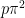(sharp).
The case p=1 is standard and follows from Wirtinger’s Inequality.
Are any inequalities like this known?
19th May 2009, 03:41 pm
Guest post by Lee Newberg [but see Comment below]
I stumbled across an old Math Chat column of yours, which mentioned that the number of ways to make change for a dollar is the coefficient of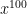 
in the Taylor expansion of
.
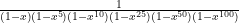But I don’t see there, or anywhere on the web, the general formula for the number of ways c(n) to make change for n dollars. In case you are interested, below I derive it to be:
.
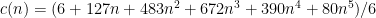Spending 1 trillion dollars with the federal stimulus means that Obama has
= 13 333333 333398 333333 333445 333333 333413 833333 333354 500000 000001
ways to make Change for America. Continue reading ‘Making Change for America’ »
18th March 2009, 09:41 am
Announcing the debut of a new AMS Graduate Student Blog by the American Mathematical Society, with a graduate student editorial board, entries ranging from “Finding an Advisor” to “Advice for the TA,” and comments invited. We are still inviting nominations and self-nominations to the graduate student editorial board, which we would like to be large and diverse.
Frank Morgan, Vice-President, AMS
with density 
and the isoperimetric problem: to enclose given weighted area with least weighted perimeter. We’ve proved that there are angles 
such that the minimizer is:
, a circular arc about the origin;
, an unduloid (half-period of a periodic curve normal to both edges of the sector);
, a semicircle through the origin.
and 
, but we have not been able to prove it. Can you help us? Check out our
Welcome to my blog. I also have a blog at the