20th April 2011, 03:59 am
Mathematics is prospering in Vietnam, supported by the latest technology. Most classrooms have built-in computer projection, and they readily supply document cameras and wireless lavaliere mikes. The internet is reliable and readily available. They’ve even figured out how to block Facebook.

Talk on “Soap Bubbles and Mathematics” to 1000 students in Thai Nguyen covered on TV.
Also see TV coverage of Hue talks.
4th April 2011, 01:16 pm
When friends hear that I’m on a math visit to Pakistan, they often say something about safety. Actually, despite heightened security, I’ve felt completely safe and at home here. The culminating experience was setting up my computer well before talks at QAU, NUST, and GCU* and finding I could leave it unattended, rarely the case in the US or anywhere else.
Incidentally, as of 2008-09, 46% of undergraduates in Pakistan are women, up from 37% in 2001-02. During this period total enrollment has more than doubled. Similarly 31% of PhD students are women, up from 20%.
*See the article by Loring Tu on the GCU “Abdus Salam School of Mathematical Sciences in Pakistan” in the August 2011 Notices of the American Mathematical Society.
4th April 2011, 09:15 am
The most important lemma of regularity for an m-dimensional area-minimizing surface S in Rn is the monotonicity of the mass ratio about a point p of S, i.e., the ratio of the area inside an n-ball about p of radius r to the volume of an m-ball of radius r [FF, Thm. 9.13 and proof], [M, 9.3]. Here in Lahore, Pakistan, at the Abdus Salam School of Mathematical Sciences, Rein Zeinstra told me that such monotonicity generalizes a similar result by Lelong [L] for complex analytic varieties (which are area minimizing). Similarly, the compactness theorem of geometric measure theory generalizes a later such result for complex analytic varieties. See a Math Review by Stoll.
[FF] Herbert Federer and Wendell H. Fleming, Normal and integral currents, Ann. of Math. 72 (1960), 458-520.
[L] Pierre Lelong, Propriétés métriques des variétés analytiques complexes définies par une équation, Ann. Sci. École Norm. Sup. 67 (1950), 393–419.
[M] Frank Morgan, Geometric Measure Theory: a Beginner’s Guide, Academic Press, 4th ed., 2009.
Category:
Math |
Comments Off on Monotoncity from Lelong to Federer-Fleming
29th March 2011, 01:21 pm
In Section 3 of his article on “Crystals, Proteins, Stability and Isoperimetry” in the April 2011 Bulletin of the American Mathematical Society, Misha Gromov suggests that a complex subvariety S of a Kähler manifold X minimizes a curvature energy defined as the volume of the unit tangent bundle S′ in the Grassmannian bundle X′ of X. Here we note that this holds for complex curves in the following sense:
Proposition. Let S be a complex curve in Cn. Then compact portions of S minimize curvature energy among surfaces (rectifiable currents) with the same boundary and the same tangent planes (almost everywhere) along the boundary.
Proof. The Grassmannian bundle is a Kähler manifold, and S′ is a complex curve, hence volume minimizing for given homology class and boundary, which corresponds to boundary and tangent planes along the boundary for S.
For example {x2=y3} in C2, with that interesting singularity at the origin. I don’t know what condition on a more general Kähler manifold X guarantees that X′ is a Kähler manifold.
Incidentally, there is a recent arXiv post on “Willmore minimizers with prescribed isoperimetric ratio” by Johannes Schygulla.
Category:
Math |
Comments Off on Complex Curves Minimize Curvature
23rd March 2011, 08:37 am
Barbosa and do Carmo [BdC] proved that a compact, stable, oriented, immersed constant-mean-curvature surface S in R3 is umbilic and hence a round sphere. The proof works for hypersurfaces in Rn as well. The proof was simplified by Wente [W], generalized to cones by Morgan and Ritoré [MR], incorrectly generalized to warped products by Montiel [M], and generalized to smooth elliptic integrands by Palmer [P]. Tashiro [T] generalized the fact that umbilic hypersurfaces are round. Locally constant normal variations show that stable implies connected.
Here we give a streamlined version of the proof without passing through the Minkowski formulae. Continue reading ‘Stable Immersions Round’ »
Category:
Math |
Comments Off on Stable Immersions Round
22nd March 2011, 05:37 pm
Guest post by Dr. Doug Corey, Department of Mathematics Education, BYU
Can you calculate the speed of light in water using only a ruler, a laser pointer, and a cup of water topped with plastic wrap (or a piece of an overhead transparency)? OK, you may need a little calculus as well, or if you are really clever you can do it with just trigonometry.
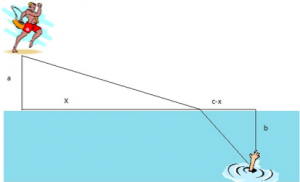 Continue reading ‘The Speed of Light in Water’ »
Continue reading ‘The Speed of Light in Water’ »
15th March 2011, 07:00 am
[“Soap Bubbles and Mathematics,” written for the Spanish Math Carnival]
¿Por qué son las pompas de jabón tan perfectamente redondas?

Continue reading ‘Pompas de Jabón y las Matemáticas’ »
21st February 2011, 04:19 pm
An interesting class of densities for the isoperimetric problem on Rn is exp(±ra). The Log-convex Density Conjecture says that spheres about the origin are isoperimetric if and only if 0≤a≤1 with the minus sign or a ≥ 1 with the plus sign, known for a=2 [Borell; see Rosales et al.] and in R2 for a≥2 [Maurmann-Morgan]. Henceforth we’ll focus on R2. Continue reading ‘Density exp(±r^a)’ »
20th February 2011, 02:50 pm
Category:
General interest |
Comments Off on Thurston to Speak at Bridges Conference in July
15th February 2011, 10:54 am
Rodrigo Banuelos suggested studying the isoperimetric problem for the radial density 1/(1+r2) corresponding to the square root of the Laplacian just as the most important Gaussian density corresponds to the Laplacian itself.
Proposition. Consider Rn with density 1/(1+r2). For n > 1 minimizers of perimeter for given volume do not exist: the perimeter can go to zero as the region goes off to infinity. On the line, for more than half the volume the minimizer is a ball about the origin, for less than half, the complement, for exactly half, the ball, its complement, or a half-line. In particular, balls about the origin are minimizing while stable, up to radius 1, with (log density)” = 2(x2-1)/(x2+1)2. Continue reading ‘Density 1/(1+r^2)’ »
Category:
Math |
Comments Off on Density 1/(1+r^2)




 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the