Frank Morgan

I traveled to Shanghai in February 2019 to teach a 10-day research seminar for the Institute for Advanced Research for what turned out to be just five high school students. At breakneck pace, I provided an introduction to Riemannian Geometry, including Gauss, sectional, Ricci, and scalar curvature, General Relativity, the Gauss-Bonnet Theorem, geodesics, and general norms. In addition, the students undertook an original research project, resulting in a published paper  on “Isoperimetric Problems on the Line with Density |x|^p”  Continue reading ‘China’ »

Nat Sothanaphan wrote this article in Grade 12.

Urinal Problem

In my Discrete Math class today, Ryan Patton asked to prove Euler’s circuit theorem by induction on the number of vertices. Alex Summers contributed an idea about pairing/short-cutting instead of removing the edges incident to a deleted vertex. The class came up with the following proof. Is this proof out there somewhere?

Theorem (Euler). A pseudograph has a circuit containing all edges and vertices if it is connected and every vertex has even degree.

Proof by induction on the number n of vertices.

Base case n=1. Just follow the loops in succession.

Now assume for n and prove for a pseudo-graph of n+1 vertices. Pick a vertex. Since degree even, you can pair the incident edges, and you can avoid pairing the two ends of a loop. Short-cut each pair to avoid the vertex and delete it. By induction, each component of the new pseudo-graph has the desired circuit. Now restore the vertex and undo the short cuts to obtain the desired circuit.

Relaxed Disk Packings

by John Berry, Matthew Dannenberg, Jason Liang, and Yengyi Zeng
2015 NSF “SMALL” undergraduate research Geometry Group

With update below by Iglesias-Ham (all already known).

Abstract. The classic result about the optimal hexagonal packing of unit disks in the plane has recently been partially generalized by Edelsbrunner et al. to allow but penalize overlap for the case of lattice packings. We attempt to remove the restriction to lattice packings. Continue reading ‘Relaxed Disk Packings’ »

Updated with new discoveries 31 January —11 February 2015 and 3 April 2019; first published 27 May 2014. (Incidentally, new type of pentagonal tile discovered July 2015 by Casey Mann, Jennifer McLoud-Mann, and David Von Derauc. And that’s it, as proved July 2017 by Michaël Rao, arX). For these examples and a proof that symmetry groups with order three rotations cannot occur, see John Berry, Matthew Dannenberg, Jason Liang, Yingyi Zeng, Symmetries of Cairo-Prismatic tilings, Rose-Hulman Und. Math. J. 17 (2016), http://scholar.rose-hulman.edu/rhumj/vol17/iss2/3.

A joint paper [C1] with my SMALL undergraduate research Geometry Group found least-perimeter pentagonal unit-area tiles, Cairo and Prismatic:

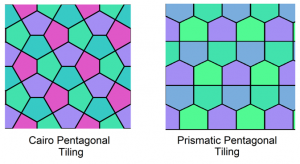They proved that mixtures of unit-area convex pentagonal tiles can do no better, but found many examples of Cairo-Prismatic tilings that do equally well [C1, C2], one appearing in the new Math Library at Williams:

Since their work nine more have been discovered.  Continue reading ‘New Optimal Pentagonal Tilings’ »

Just as a a soap bubble minimizes surface area, crystals minimize a more general energy depending on orientation with respect to the underlying crystal lattice, given by integrating some (continuous) norm on the unit normal. (One might drop the usual assumption that a norm is even.) The optimal shape is the unit ball of the dual norm, called the Wulff crystal (see [M2, Chapt. 16]). Continue reading ‘Clusters for General Norms’ »

Enjoying a conference on isoperimetric problems in Pisa. (Click on image to enlarge.)

Continue reading ‘Isoperimetric Problems in Pisa’ »

I’m speaking at a CIME school at the truly Grand Hotel San Michele on the Italian coast, kindly organized by Alberto Farina and Enrico Valdinoci. The path from the hotel to the private beachclub is rather dramatic. It begins with a long descent down the front stairs and another long stairway under the highway.

Continue reading ‘Grand Hotel San Michele’ »

I just had a great time at the amazing conference for 800 top Indian high school science students. Here I provide some contacts and information for my young new Indian friends and all; some pictures, including some wonderful pentagonal tilings I found on the path to the Guest House, the ever busy and calm organizer Kaushal Verma, and my student host Devang Rammohan, who met me at the airport at 5 am and took me back at midnight. I’m grateful to all the organizers and participants for their role in this inspiring vision of the future of science in India and beyond. Continue reading ‘Indian Science Camp’ »

Emanuel Milman [M2, 2013] provides very general sharp lower bounds on perimeter to enclose prescribed volume, including the following special case of convex bodies in Rⁿ. Here we give an alternative proof for that special case as suggested by Milman [M2, §7.2]. For sharp upper bounds see my post [Mo1] on the Convex Body Isoperimetric Conjecture. Continue reading ‘Sharp Isoperimetric Bounds for Convex Bodies’ »