Sharp Isoperimetric Bounds for Convex Bodies
Emanuel Milman [M2, 2013] provides very general sharp lower bounds on perimeter to enclose prescribed volume, including the following special case of convex bodies in Rn. Here we give an alternative proof for that special case as suggested by Milman [M2, §7.2]. For sharp upper bounds see my post [Mo1] on the Convex Body Isoperimetric Conjecture.
2.1. Theorem [M2, Cor. 1.4, Case p = 0]. Let K be an open convex body in Rn (n≥2) of volume V and diameter d. Let R be a subset of K with volume sV (0 < s ≤ 1/2). Then the area A of the boundary of R in K satisfies:
A > (V/d)An(s) ≥ (V/d)A∞(s),
where
An(s) = n min {[s(b+1)n + (1-s)bn](n-1)/n/[(b+1)n–bn] : b ≥ 0},
A∞(s) = min {[saen + (1-s)a]/[ea-1] : a ≥ 0},
In particular, for n = 2 (where A denotes length and V denotes area),
A > (2V/d)√(s(1-s)).
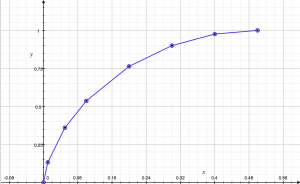
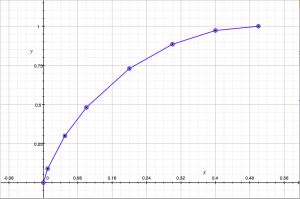
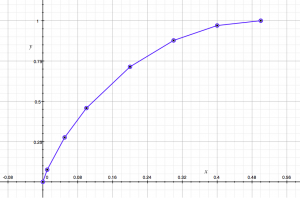
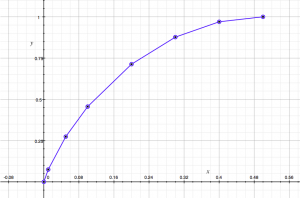
The lower bound An(s) is nonincreasing in n and sharp for every s and d (as V approaches 0). See Figure 1.
Figure 1. Graphs of the sharp lower bounds An(s) for n = 3, 8, 100, ∞. These bounds are concave and decreasing in n.
Remarks. One checks that A∞(1/2) = 1. Considering b→0 shows that An(1/2) ≤ 1 and hence must equal 1/2. Since the quantities minimized are concave, the minima An(s) and A∞(s) are concave. In particular, A∞(s) ≥ 2s, the previous result of Dyer and Frieze [DF, §4.3, 1991], with subtle refinements by Kannan et al. [KLS, 1995], Bobkov [B], Milman [M1], and Steinerberger [S, 2013]. The earlier estimate A ≥ sV/d [KK, Thm. 2, 1991] is relatively trivial modulo a little geometric measure theory. Barthe [Ba, Prop. 11] provided the excellent but not sharp lower bound (2V/d0)(√s + √(1–s)–1) if K is contained in a ball of diameter d0.
Proof. By scaling we may assume that d = 1. We apply repeated subdivision after Payne-Weinberger and Lovász-Simonovits ([PW], [LS, §2], cited by Milman [M3, §7.2]) as described in Gromov [G, 3.5.27], which can be consulted for further detail. Remove a small ε neighborhood of ∂R, of volume γV, leaving parts of R and K–R of volumes αV and βV separated by distance 2ε. Of course α + β + γ = 1. By the Ham-Sandwich Theorem there is a hyperplane with unit normal in any prescribed circle of directions that cuts both parts in half. Take the half K2 of K with smaller total volume, with parts of R and K–R of volumes αV/2 and βV/2, separated by distance at least 2ε by a region occupying volume γ2V/2 ≤ γV/2. Keep repeating. One can choose the hyperplanes so that the limit is a line segment, of length at most 1, with an inherited density, normalized to unit mass, and two parts of mass α∞ and β∞ in the same ratio as α and β separated by distance at least 2ε by set of mass γ∞ = 1–α∞–β∞ ≤ γ. The 1/n power of such a density must be concave. The minimum is attained by an interval on a segment of length 1 with a density of the form (a(x+b))n on [0, 1] or equivalently (ax)n on [b, b+1], with unit mass.
As ε→0, γV/2ε converges to the area (Minkowski content) A of ∂R and α and β converge to s and 1–s. Meanwhile the lower bound on γ/2ε ≥ γ∞/2ε subconverges to the mass of a point separating the unit segment into pieces of mass s and 1–s, the minimum given by (ac)n, where the weighted measure of [b, c] is s and the weighted measure of [c, b+1] is 1-s. Using these two constraints to eliminate the parameters a and c yields the first lower bound An. By construction An is nonincreasing in n. Since for small V the weighted segments are approximated by thin convex bodies or “needles”, An is a sharp lower bound. The inequality is strict, because not all such needles can have unit diameter. For the case n = 2, one can compute A2(s) as stated.
To obtain the weaker bound A∞(s), note that all of these densities are log concave, for which the lower bound is given by eax on [b, b+1]. This time it is easier to use the constraints to eliminate the parameters b and c, yielding the second, weaker lower bound A∞(s).
Remark. Choe et al. ([ChGR]; see also [Mo3]) provide an isoperimetric inequality in the complement of a convex body.
Remark. Geometric measure theory (see e.g. [Mo2]) provides inside an open convex body in Rn a region of given volume fraction and minimum perimeter. The interface is a constant-mean-curvature hypersurface, smooth except possibly for a singular set of Hausdorff dimension at most n–8. If the convex body has a smooth boundary, then the interface is smooth at the boundary.
References
[Ba] F. Barthe, Log-concave and spherical models in isoperimetry, Geom. Funct. Anal. 12 (2002), 32-55.
[Bo] S. Bobkov, On isoperimetric constants for log-concave probability distributions, Geometric Aspects of Functional Analysis, Israel Seminar 2004-2005, Lectures Notes in Math. 1910, Springer, Berlin, 2007, 81-88.
[ChGR] Jaigyoung Choe, Mohammad Ghomi, and Manuel Ritoré, The relative isoperimetric inequality outside convex domains in Rn. Calc. Var. Partial Differential Equations 29 (2007), 421-429.
[DF] Martin Dyer and Alan Frieze, Computing the volume of convex bodies: a case where randomness provably helps, Proc. Symp. Applied Math 44 (1991), 123-169.
[G] Misha Gromov, Metric Structures for Riemannian and Non-Riemannian Spaces, Progress in Math. 152, Birkhäuser, second printing, 2001.
[KLS] Ravi Kannan, László Lovász, and Miklós Simonovits, Isoperimetric problems for convex bodies and a localization lemma, Discrete Comput. Geom. 13 (1995), 541–559.
[KK] Alexander Karzanov and Leonid Khachiyan, On the conductance of order Markov chains, Order 8 (1991), 7-15.
[LS] László Lovász, and Miklós Simonovits, The mixing rate of Markov chains, an isoperimetric inequality, and computing the volume, 31st Annual Symposium on Foundations of Computer Science, Vol. I, II (St. Louis, MO, 1990), 346–354, IEEE Comput. Soc. Press, Los Alamitos, CA, 1990.
[M1] Emanuel Milman, Isoperimetric bounds on convex manifolds, Christian Houdré, Michel Ledoux, Emanuel Milman, and Mario Milman, eds., Concentration, Functional Inequalities and Isoperimetry, Contemporary Math. 545 (2011), 195-208.
[M2] Emanuel Milman, Sharp isoperimetric inequalities and model spaces of curvature-dimension-diameter condition, http://arxiv.org/abs/1108.4609v1.
[Mo1] Frank Morgan, Convex body isoperimetric conjecture, Morgan blog.
[Mo2] Frank Morgan, Geometric Measure Theory: a Beginner’s Guide, Academic Press, 4th edition, 2009.
[Mo3] Frank Morgan, Isoperimetric inequality in complement of mean convex set fails at Banff, Morgan blog.
[PW] L. E. Payne and H. F. Weinberger, An optimal Poincaré inequality for convex domains, Arch. Rational Mech. Anal. 5 (1960), 286–292.
[S] Stefan Steinerberger, The optimal L1-Poincaré inequality and some isoperimetric applications, http://arxiv.org/abs/1309.6211
 Welcome to my blog. I also have a blog at the
Welcome to my blog. I also have a blog at the
Frank Morgan » Blog Archive » Convex Body Isoperimetric Conjecture:
[…] 5. For sharp lower bounds, see my post Sharp Isoperimetric Bounds for Convex Bodies. […]
30 October 2013, 2:31 pm